310386: CF1825E. LuoTianyi and XOR-Tree

E. LuoTianyi and XOR-Treetime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

LuoTianyi gives you a tree with values in its vertices, and the root of the tree is vertex $1$.

In one operation, you can change the value in one vertex to any non-negative integer.

Now you need to find the minimum number of operations you need to perform to make each path from the root to leaf$^{\dagger}$ has a bitwise XOR value of zero.

$^{\dagger}$A leaf in a rooted tree is a vertex that has exactly one neighbor and is not a root.

Input

The first line contains a single integer $n$ ($2 \le n \le 10^5$) — the number of vertices in the tree.

The second line contains $n$ integers $a_1, a_2, \ldots, a_n$ ($1 \le a_i \le 10^9$), the $i$-th number represents the value in the $i$-th vertex.

Next $n−1$ lines describe the edges of the tree. The $i$-th line contains two integers $u_i$ and $v_i$ ($1 \le u_i,v_i \le n, u_i \neq v_i$) — the vertices connected by an edge of the tree. It's guaranteed that the given edges form a tree.

Output

Print a single integer — the minimum number of operations.

ExamplesInput

6
3 5 7 5 8 4
1 2
1 3
1 4
3 5
4 6

Output

3

Input

8
7 10 7 16 19 9 16 11
1 5
4 2
6 5
5 2
7 2
2 3
3 8

Output

3

Input

4
1 2 1 2
1 2
2 3
4 3

Output

0

Input

9
4 3 6 1 5 5 5 2 7
1 2
2 3
4 1
4 5
4 6
4 7
8 1
8 9

Output

2

Note

The tree in the first example:

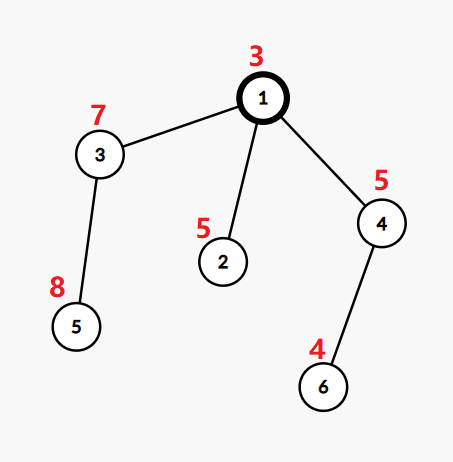
If we change the value in the vertex $2$ to $3$, the value in the vertex $5$ to $4$, and the value in the vertex $6$ to $6$, then the tree will be ok.

The bitwise XOR from the root to the leaf $2$ will be $3 \oplus 3=0$.

The bitwise XOR from the root to the leaf $5$ will be $4 \oplus 7 \oplus 3=0$.

The bitwise XOR from the root to the leaf $6$ will be $6 \oplus 5 \oplus 3=0$.

The tree in the second example:

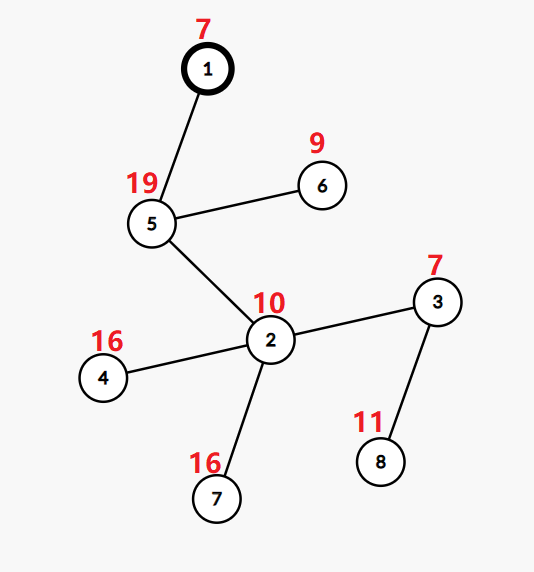
If we change the value in the vertex $2$ to $4$, the value in the vertex $3$ to $27$, and the value in the vertex $6$ to $20$, then the tree will be ok.

The bitwise XOR from the root to the leaf $6$ will be $20 \oplus 19 \oplus 7=0$.

The bitwise XOR from the root to the leaf $8$ will be $11 \oplus 27 \oplus 4 \oplus 19 \oplus 7=0$.

The bitwise XOR from the root to the leaf $4$ will be $16 \oplus 4 \oplus 19 \oplus 7=0$.

The bitwise XOR from the root to the leaf $7$ will be $16 \oplus 4 \oplus 19 \oplus 7=0$.

In the third example, the only leaf is the vertex $4$ and the bitwise XOR on the path to it is $1 \oplus 2 \oplus 1 \oplus 2 = 0$, so we don't need to change values.

In the fourth example, we can change the value in the vertex $1$ to $5$, and the value in the vertex $4$ to $0$.

Here $\oplus$ denotes the bitwise XOR operation.

题目大意：给定一个以1号顶点为根的树，每个顶点有一个值。可以通过一次操作将某个顶点的值改变为任何非负整数。要求通过最少的操作次数，使得从根到每个叶子节点的路径上的按位异或（XOR）值为零。

输入数据格式：
- 第一行一个整数n（2≤n≤10^5），表示顶点的数量。
- 第二行n个整数a_1, a_2, ..., a_n（1≤a_i≤10^9），分别表示每个顶点的值。
- 接下来n-1行，每行两个整数u_i和v_i（1≤u_i,v_i≤n, u_i≠v_i），表示树中的一条边。

输出数据格式：
- 输出一个整数，表示所需的最少操作次数。

示例输入输出已给出，具体见题目描述。

公式使用LaTeX格式表示，例如按位异或操作表示为 $ a \oplus b $。题目大意：给定一个以1号顶点为根的树，每个顶点有一个值。可以通过一次操作将某个顶点的值改变为任何非负整数。要求通过最少的操作次数，使得从根到每个叶子节点的路径上的按位异或（XOR）值为零。 输入数据格式： - 第一行一个整数n（2≤n≤10^5），表示顶点的数量。 - 第二行n个整数a_1, a_2, ..., a_n（1≤a_i≤10^9），分别表示每个顶点的值。 - 接下来n-1行，每行两个整数u_i和v_i（1≤u_i,v_i≤n, u_i≠v_i），表示树中的一条边。 输出数据格式： - 输出一个整数，表示所需的最少操作次数。 示例输入输出已给出，具体见题目描述。 公式使用LaTeX格式表示，例如按位异或操作表示为 $ a \oplus b $。