310380: CF1824E. LuoTianyi and Cartridge
Description
LuoTianyi is watching the anime Made in Abyss. She finds that making a Cartridge is interesting. To describe the process of making a Cartridge more clearly, she abstracts the original problem and gives you the following problem.
You are given a tree $T$ consisting of $n$ vertices. Each vertex has values $a_i$ and $b_i$ and each edge has values $c_j$ and $d_j$.
Now you are aim to build a tree $T'$ as follows:
- First, select $p$ vertices from $T$ ($p$ is a number chosen by yourself) as the vertex set $S'$ of $T'$.
- Next, select $p-1$ edges from $T$ one by one (you cannot select one edge more than once).
- May you have chosen the $j$-th edge connects vertices $x_j$ and $y_j$ with values $(c_j,d_j)$, then you can choose two vertices $u$ and $v$ in $S'$ that satisfy the edge $(x_j,y_j)$ is contained in the simple path from $u$ to $v$ in $T$, and link $u$ and $v$ in $T'$ by the edge with values $(c_j,d_j)$ ($u$ and $v$ shouldn't be contained in one connected component before in $T'$).
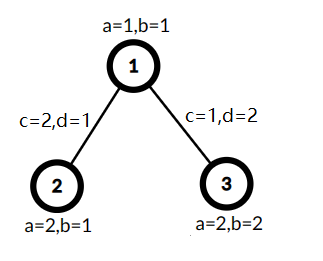 A tree with three vertices, $\min(A,C)=1,B+D=7$, the cost is $7$.
A tree with three vertices, $\min(A,C)=1,B+D=7$, the cost is $7$. 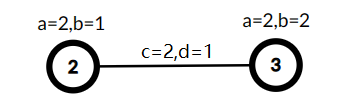 Selected vertices $2$ and $3$ as $S'$, used the edge $(1,2)$ with $c_j = 2$ and $d_j = 1$ to link this vertices, now $\min(A,C)=2,B+D=4$, the cost is $8$.
Selected vertices $2$ and $3$ as $S'$, used the edge $(1,2)$ with $c_j = 2$ and $d_j = 1$ to link this vertices, now $\min(A,C)=2,B+D=4$, the cost is $8$. Let $A$ be the minimum of values $a_i$ in $T'$ and $C$ be the minimum of values $c_i$ in $T'$. Let $B$ be the sum of $b_i$ in $T'$ and $D$ be the sum of values $d_i$ in $T'$. Let $\min(A, C) \cdot (B + D)$ be the cost of $T'$. You need to find the maximum possible cost of $T'$.
InputThe first line contains one integer $n$ ($3\le n \le 2\cdot 10^5$) — the number of vertices in the tree $T$.
The second line contains $n$ integers $a_1, a_2, \ldots, a_n$ ($1\le a_i\le 2\cdot 10^5$), where the $i$-th integer represents the $a_i$ value of the $i$-th vertex.
The third line contains $n$ integers $b_1, b_2, \ldots, b_n$ ($1\le b_i\le 2\cdot 10^5$), where the $i$-th integer represents the $b_i$ value of the $i$-th vertex.
Then $n-1$ lines follow, the $j$-th of them contains four integers $x_j,y_j,c_j,d_j$ ($1\le x_j,y_j\le n,1\le c_j,d_j\le 2\cdot 10^5$) representing the edge $(x_j,y_j)$ and its values $c_j$ and $d_j$ respectively. It's guaranteed that edges form a tree.
OutputPrint a single integer — the maximum possible cost of $T'$.
ExamplesInput3 1 2 2 1 1 2 1 2 2 1 1 3 1 2Output
8Input
5 2 4 2 1 1 2 4 4 4 4 2 5 3 3 3 5 2 4 4 2 5 5 5 1 1 5Output
35Input
6 5 7 10 7 9 4 6 9 7 9 8 5 2 1 5 1 3 2 2 4 4 3 6 3 5 1 7 4 6 5 6 8Output
216Input
5 1000 1000 1 1000 1000 1000 1000 1 1000 1000 1 2 1 1 2 3 1000 1000 3 4 1000 1000 3 5 1000 1000Output
7000000Note
The tree from the first example is shown in the statement.
The tree from the second example is shown below:
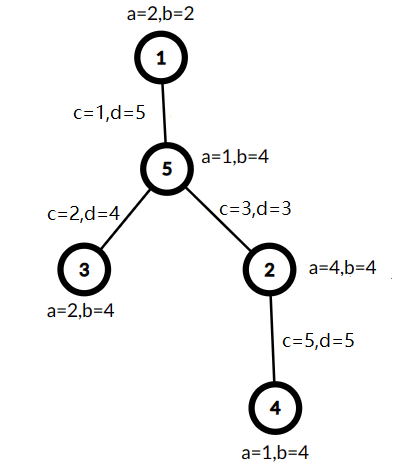
$A = 1, B = 18, C = 1, D = 17$, so the cost is $\min(1,1) \cdot (18 + 17) = 35$.
Input
题意翻译
### 题目描述 给定一棵 $n$ 个结点的树 $T$,点有点权 $a_i, b_i$,边有边权 $c_i, d_i$。 按如下方式构建另一棵树 $T'$: - 选择 $T$ 的 $p$ 个结点作为 $T'$ 的点集 $V'$。$p$ 可以是 $1\sim n$ 的任意正整数。 - 接下来 **依次** 选择 $T$ 的 $p - 1$ 条 **互不相同** 的边。 - 对于第 $i$ 次选边,假设选择第 $j$ 条边 $(x_j, y_j)$,那么你可以选择 $V'$ 的 **不连通** 的两个点 $u, v$,要求 $(x_j, y_j)$ 包含于 $u, v$ 在 $T$ 上的简单路径,在 $u, v$ 之间以 $c_j, d_j$ 为权值连边。 设 $A, C$ 分别为 $T'$ 的 $a_i, c_i$ 的最小值,$B, D$ 分别为 $T'$ 的 $b_i, d_i$ 之和,则 $T'$ 的权值为 $\min(A, C)\cdot (B + D)$。 求 $T'$ 的最大权值。 $3\leq n\leq 2\times 10 ^ 5$,$1\leq a_i, b_i, c_i, d_i\leq 2\times 10 ^ 5$,保证 $(x_i, y_i)$ 形成一棵树。 ### 输入格式 第一行一个正整数 $n$。 第二行 $n$ 个正整数 $a_i$。 第三行 $n$ 个正整数 $b_i$。 接下来 $n - 1$ 行,每行四个正整数 $x_i, y_i, c_i, d_i$。 ### 输出格式 输出一行一个整数表示答案 —— $T'$ 的最大权值。 翻译提供者:[Alex_Wei](https://www.luogu.com.cn/user/123294)。Output
时间限制:每个测试用例3秒
内存限制:每个测试用例1024兆字节
输入:标准输入
输出:标准输出
题目大意:
洛天依正在看动漫《来自深渊》。她发现制作一个墨盒很有趣。为了更清楚地描述制作墨盒的过程,她将原问题抽象化,并给出了以下问题。
你有一颗包含n个顶点的树T。每个顶点都有值a_i和b_i,每条边都有值c_j和d_j。
现在你要构建一棵树T',如下所示:
1. 首先,从T中选择p个顶点(p由你自己选择)作为T'的顶点集S'。
2. 接下来,从T中逐个选择p-1条边(你不能多次选择同一条边)。
3. 如果你选择了第j条边,它连接了顶点x_j和y_j,并具有值(c_j,d_j),则你可以选择S'中的两个顶点u和v,使得边(x_j,y_j)包含在T中从u到v的简单路径上,并通过具有值(c_j,d_j)的边将u和v在T'中连接起来(u和v之前不应包含在T'的一个连通分量中)。
定义A为T'中a_i的最小值,C为T'中c_i的最小值。定义B为T'中b_i的和,D为T'中d_i的和。定义min(A,C) * (B+D)为T'的成本。你需要找到T'可能的最大成本。
输入格式:
第一行包含一个整数n(3≤n≤2*10^5)——树T的顶点数。
第二行包含n个整数a_1, a_2, ..., a_n(1≤a_i≤2*10^5),其中第i个整数表示第i个顶点的a_i值。
第三行包含n个整数b_1, b_2, ..., b_n(1≤b_i≤2*10^5),其中第i个整数表示第i个顶点的b_i值。
然后是n-1行,第j行包含四个整数x_j,y_j,c_j,d_j(1≤x_j,y_j≤n,1≤c_j,d_j≤2*10^5),分别表示边(x_j,y_j)及其值c_j和d_j。保证边构成一棵树。
输出格式:
打印一个整数——T'可能的最大成本。洛天依和墨盒 时间限制:每个测试用例3秒 内存限制:每个测试用例1024兆字节 输入:标准输入 输出:标准输出 题目大意: 洛天依正在看动漫《来自深渊》。她发现制作一个墨盒很有趣。为了更清楚地描述制作墨盒的过程,她将原问题抽象化,并给出了以下问题。 你有一颗包含n个顶点的树T。每个顶点都有值a_i和b_i,每条边都有值c_j和d_j。 现在你要构建一棵树T',如下所示: 1. 首先,从T中选择p个顶点(p由你自己选择)作为T'的顶点集S'。 2. 接下来,从T中逐个选择p-1条边(你不能多次选择同一条边)。 3. 如果你选择了第j条边,它连接了顶点x_j和y_j,并具有值(c_j,d_j),则你可以选择S'中的两个顶点u和v,使得边(x_j,y_j)包含在T中从u到v的简单路径上,并通过具有值(c_j,d_j)的边将u和v在T'中连接起来(u和v之前不应包含在T'的一个连通分量中)。 定义A为T'中a_i的最小值,C为T'中c_i的最小值。定义B为T'中b_i的和,D为T'中d_i的和。定义min(A,C) * (B+D)为T'的成本。你需要找到T'可能的最大成本。 输入格式: 第一行包含一个整数n(3≤n≤2*10^5)——树T的顶点数。 第二行包含n个整数a_1, a_2, ..., a_n(1≤a_i≤2*10^5),其中第i个整数表示第i个顶点的a_i值。 第三行包含n个整数b_1, b_2, ..., b_n(1≤b_i≤2*10^5),其中第i个整数表示第i个顶点的b_i值。 然后是n-1行,第j行包含四个整数x_j,y_j,c_j,d_j(1≤x_j,y_j≤n,1≤c_j,d_j≤2*10^5),分别表示边(x_j,y_j)及其值c_j和d_j。保证边构成一棵树。 输出格式: 打印一个整数——T'可能的最大成本。