309821: CF1740G. Dangerous Laser Power
Memory Limit:512 MB
Time Limit:4 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Dangerous Laser Power
题意翻译
给出一个 $n \times m(n,m \leq 1000)$ 的矩阵 $a$,现在要给每个格子分配一个01变量 $t_{i,j}$。考虑从某个格子的某个边界射入一道激光,维护初始是 $1$ 的前缀最大值,进入一个格子的时候chkmax,把增量计入这个格子的贡献。如果 $t_{i,j} = 1$ 则右转,否则直行。激光遇到环或者离开矩阵的时候消失。对所有 $4nm$ 种选起点的方式求出每个格子的贡献和。如果这个数和 $t_{i,j}$ 奇偶性相同则称这是一个好格子。最大化好格子的数量。题目描述
Pak Chanek has an $ n \times m $ grid of portals. The portal on the $ i $ -th row and $ j $ -th column is denoted as portal $ (i,j) $ . The portals $ (1,1) $ and $ (n,m) $ are on the north-west and south-east corner of the grid respectively. The portal $ (i,j) $ has two settings: - Type $ t_{i,j} $ , which is either $ 0 $ or $ 1 $ . - Strength $ s_{i,j} $ , which is an integer between $ 1 $ and $ 10^9 $ inclusive. Each portal has $ 4 $ faces labelled with integers $ 0,1,2,3 $ , which correspond to the north, east, south, and west direction respectively. 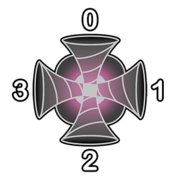When a laser enters face $ k $ of portal $ (i, j) $ with speed $ x_\text{in} $ , it leaves the portal going out of face $ (k+2+t_{i,j}) \bmod 4 $ with speed $ x_\text{out} = \max(x_\text{in},s_{i,j}) $ . The portal also has to consume $ x_\text{out} - x_\text{in} $ units of energy. Pak Chanek is very bored today. He will shoot $ 4nm $ lasers with an initial speed of $ 1 $ , one into each face of each portal. Each laser will travel throughout this grid of portals until it moves outside the grid or it has passed through $ 10^{100} $ portals. At the end, Pak Chanek thinks that a portal is good if and only if the total energy consumed by that portal modulo $ 2 $ is equal to its type. Given the strength settings of all portals, find a way to assign the type settings of each portal such that the number of good portals is maximised.输入输出格式
输入格式
The first line contains two integers $ n $ and $ m $ ( $ 1 \le n, m \le 1000 $ ) — the number of rows and columns in the grid. The $ i $ -th of the next $ n $ lines contains $ m $ integers, with the $ j $ -th integer being $ s_{i,j} $ ( $ 1 \leq s_{i,j} \leq 10^9 $ ) — the strength of portal $ (i, j) $ .
输出格式
Print $ n $ lines with each line containing a string of length $ m $ consisting of characters $ 0 $ or $ 1 $ representing the type settings. The $ j $ -th character in the $ i $ -th string is the type setting of portal $ (i, j) $ . If there are multiple solutions, you can output any of them.
输入输出样例
输入样例 #1
2 3
8 8 2
6 5 7输出样例 #1
110
100输入样例 #2
1 2
420 69输出样例 #2
10说明
In the first example, let's consider the laser Pak Chanek shoots into face $ 1 $ of portal $ (2, 2) $ . The laser travels as follows: 1. The laser enters face $ 1 $ of portal $ (2, 2) $ with speed $ 1 $ . It leaves the portal going out of face $ 3 $ with speed $ 5 $ . Portal $ (2, 2) $ consumes $ 4 $ units of energy. 2. The laser enters face $ 1 $ of portal $ (2, 1) $ with speed $ 5 $ . It leaves the portal going out of face $ 0 $ with speed $ 6 $ . Portal $ (2, 1) $ consumes $ 1 $ units of energy. 3. The laser enters face $ 2 $ of portal $ (1, 1) $ with speed $ 6 $ . It leaves the portal going out of face $ 1 $ with speed $ 8 $ . Portal $ (1, 1) $ consumes $ 2 $ units of energy. 4. The laser enters face $ 3 $ of portal $ (1, 2) $ with speed $ 8 $ . It leaves the portal going out of face $ 2 $ with speed $ 8 $ . Portal $ (1, 2) $ consumes $ 0 $ units of energy. 5. The laser enters face $ 0 $ of portal $ (2, 2) $ with speed $ 8 $ . It leaves the portal going out of face $ 2 $ with speed $ 8 $ . Portal $ (2, 2) $ consumes $ 0 $ units of energy. The illustration of the travel of the laser above is as follows. 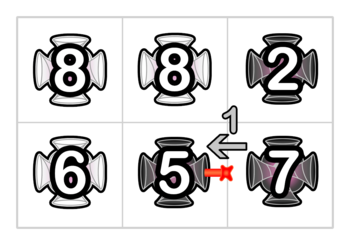As an example, consider portal $ (2, 3) $ . We can calculate that the total energy consumed by that portal in the end will be $ 32 $ . Since $ 32 \bmod 2 = 0 $ and $ t_{2,3} = 0 $ , then it is a good portal.Input
题意翻译
给出一个 $n \times m(n,m \leq 1000)$ 的矩阵 $a$,现在要给每个格子分配一个01变量 $t_{i,j}$。考虑从某个格子的某个边界射入一道激光,维护初始是 $1$ 的前缀最大值,进入一个格子的时候chkmax,把增量计入这个格子的贡献。如果 $t_{i,j} = 1$ 则右转,否则直行。激光遇到环或者离开矩阵的时候消失。对所有 $4nm$ 种选起点的方式求出每个格子的贡献和。如果这个数和 $t_{i,j}$ 奇偶性相同则称这是一个好格子。最大化好格子的数量。Output
**危险激光功率**
**题意翻译**:
有一个 $ n \times m(n,m \leq 1000) $ 的矩阵 $ a $,每个格子分配一个01变量 $ t_{i,j} $。从某个格子的某个边界射入一道激光,维护初始是 $ 1 $ 的前缀最大值,进入一个格子的时候chkmax,把增量计入这个格子的贡献。如果 $ t_{i,j} = 1 $ 则右转,否则直行。激光遇到环或者离开矩阵的时候消失。对所有 $ 4nm $ 种选起点的方式求出每个格子的贡献和。如果这个数和 $ t_{i,j} $ 奇偶性相同则称这是一个好格子。最大化好格子的数量。
**题目描述**:
Pak Chanek有一个 $ n \times m $ 的传送门网格。传送门 $ (i,j) $ 有以下设置:
- 类型 $ t_{i,j} $,值为 $ 0 $ 或 $ 1 $。
- 强度 $ s_{i,j} $,为 $ 1 $ 到 $ 10^9 $ 之间的整数。
每个传送门有四个标有整数 $ 0,1,2,3 $ 的面,分别对应北、东、南、西方向。当激光以速度 $ x_\text{in} $ 进入传送门 $ (i, j) $ 的面 $ k $ 时,它会以速度 $ x_\text{out} = \max(x_\text{in},s_{i,j}) $ 从面 $ (k+2+t_{i,j}) \bmod 4 $ 离开。传送门消耗的能量为 $ x_\text{out} - x_\text{in} $。
Pak Chanek会射出 $ 4nm $ 道初始速度为 $ 1 $ 的激光,每道激光最终会离开网格或通过 $ 10^{100} $ 个传送门。
最后,如果传送门消耗的总能量模 $ 2 $ 等于其类型,则称该传送门为好传送门。给定所有传送门的强度设置,找到一种分配传送门类型设置的方法,以最大化好传送门的数量。
**输入输出格式**:
**输入格式**:
第一行包含两个整数 $ n $ 和 $ m $($ 1 \le n, m \le 1000 $)——网格的行数和列数。
接下来的 $ n $ 行中的第 $ i $ 行包含 $ m $ 个整数,第 $ j $ 个整数为 $ s_{i,j} $($ 1 \leq s_{i,j} \leq 10^9 $)——传送门 $ (i, j) $ 的强度。
**输出格式**:
输出 $ n $ 行,每行包含一个长度为 $ m $ 的字符串,由字符 $ 0 $ 或 $ 1 $ 组成,表示传送门的类型设置。第 $ i $ 行的第 $ j $ 个字符是传送门 $ (i, j) $ 的类型设置。
如果有多个解决方案,您可以输出其中任何一个。
**输入输出样例**:
**输入样例 #1**:
```
2 3
8 8 2
6 5 7
```
**输出样例 #1**:
```
110
100
```
**输入样例 #2**:
```
1 2
420 69
```
**输出样例 #2**:
```
10
```
**说明**:
在第一个例子中,考虑Pak Chanek射入传送门 $ (2, 2) $ 面积 $ 1 $ 的激光。激光的传播如下:
1. 激光以速度 $ 1 $ 进入传送门 $ (2, 2) $ 的面 $ 1 $。它以速度 $ 5 $ 从面 $ 3 $ 离开。传送门 $ (2, 2) $ 消耗 $ 4 $ 单位的能量。
2. 激光以速度 $ 5 $ 进入传送门 $ (2, 1) $ 的面 $ 1 $。它以速度 $ 6 $ 从面 $ 0 $ 离开。传送门 $ (2, 1) $ 消耗 $ 1 $ 单位的能量。
3. 激光以速度 $ 6 $ 进入传送门 $ (1, 1) $ 的面 $ 2 $。它以速度 $ 8 $ 从面 $ 1 $ 离开。传送门 $ (1, 1) $ 消耗 $ 2 $ 单位的能量。
4. 激光以速度 $ 8 $ 进入传送门 $ (1, 2) $ 的面 $ 3**危险激光功率** **题意翻译**: 有一个 $ n \times m(n,m \leq 1000) $ 的矩阵 $ a $,每个格子分配一个01变量 $ t_{i,j} $。从某个格子的某个边界射入一道激光,维护初始是 $ 1 $ 的前缀最大值,进入一个格子的时候chkmax,把增量计入这个格子的贡献。如果 $ t_{i,j} = 1 $ 则右转,否则直行。激光遇到环或者离开矩阵的时候消失。对所有 $ 4nm $ 种选起点的方式求出每个格子的贡献和。如果这个数和 $ t_{i,j} $ 奇偶性相同则称这是一个好格子。最大化好格子的数量。 **题目描述**: Pak Chanek有一个 $ n \times m $ 的传送门网格。传送门 $ (i,j) $ 有以下设置: - 类型 $ t_{i,j} $,值为 $ 0 $ 或 $ 1 $。 - 强度 $ s_{i,j} $,为 $ 1 $ 到 $ 10^9 $ 之间的整数。 每个传送门有四个标有整数 $ 0,1,2,3 $ 的面,分别对应北、东、南、西方向。当激光以速度 $ x_\text{in} $ 进入传送门 $ (i, j) $ 的面 $ k $ 时,它会以速度 $ x_\text{out} = \max(x_\text{in},s_{i,j}) $ 从面 $ (k+2+t_{i,j}) \bmod 4 $ 离开。传送门消耗的能量为 $ x_\text{out} - x_\text{in} $。 Pak Chanek会射出 $ 4nm $ 道初始速度为 $ 1 $ 的激光,每道激光最终会离开网格或通过 $ 10^{100} $ 个传送门。 最后,如果传送门消耗的总能量模 $ 2 $ 等于其类型,则称该传送门为好传送门。给定所有传送门的强度设置,找到一种分配传送门类型设置的方法,以最大化好传送门的数量。 **输入输出格式**: **输入格式**: 第一行包含两个整数 $ n $ 和 $ m $($ 1 \le n, m \le 1000 $)——网格的行数和列数。 接下来的 $ n $ 行中的第 $ i $ 行包含 $ m $ 个整数,第 $ j $ 个整数为 $ s_{i,j} $($ 1 \leq s_{i,j} \leq 10^9 $)——传送门 $ (i, j) $ 的强度。 **输出格式**: 输出 $ n $ 行,每行包含一个长度为 $ m $ 的字符串,由字符 $ 0 $ 或 $ 1 $ 组成,表示传送门的类型设置。第 $ i $ 行的第 $ j $ 个字符是传送门 $ (i, j) $ 的类型设置。 如果有多个解决方案,您可以输出其中任何一个。 **输入输出样例**: **输入样例 #1**: ``` 2 3 8 8 2 6 5 7 ``` **输出样例 #1**: ``` 110 100 ``` **输入样例 #2**: ``` 1 2 420 69 ``` **输出样例 #2**: ``` 10 ``` **说明**: 在第一个例子中,考虑Pak Chanek射入传送门 $ (2, 2) $ 面积 $ 1 $ 的激光。激光的传播如下: 1. 激光以速度 $ 1 $ 进入传送门 $ (2, 2) $ 的面 $ 1 $。它以速度 $ 5 $ 从面 $ 3 $ 离开。传送门 $ (2, 2) $ 消耗 $ 4 $ 单位的能量。 2. 激光以速度 $ 5 $ 进入传送门 $ (2, 1) $ 的面 $ 1 $。它以速度 $ 6 $ 从面 $ 0 $ 离开。传送门 $ (2, 1) $ 消耗 $ 1 $ 单位的能量。 3. 激光以速度 $ 6 $ 进入传送门 $ (1, 1) $ 的面 $ 2 $。它以速度 $ 8 $ 从面 $ 1 $ 离开。传送门 $ (1, 1) $ 消耗 $ 2 $ 单位的能量。 4. 激光以速度 $ 8 $ 进入传送门 $ (1, 2) $ 的面 $ 3
**题意翻译**:
有一个 $ n \times m(n,m \leq 1000) $ 的矩阵 $ a $,每个格子分配一个01变量 $ t_{i,j} $。从某个格子的某个边界射入一道激光,维护初始是 $ 1 $ 的前缀最大值,进入一个格子的时候chkmax,把增量计入这个格子的贡献。如果 $ t_{i,j} = 1 $ 则右转,否则直行。激光遇到环或者离开矩阵的时候消失。对所有 $ 4nm $ 种选起点的方式求出每个格子的贡献和。如果这个数和 $ t_{i,j} $ 奇偶性相同则称这是一个好格子。最大化好格子的数量。
**题目描述**:
Pak Chanek有一个 $ n \times m $ 的传送门网格。传送门 $ (i,j) $ 有以下设置:
- 类型 $ t_{i,j} $,值为 $ 0 $ 或 $ 1 $。
- 强度 $ s_{i,j} $,为 $ 1 $ 到 $ 10^9 $ 之间的整数。
每个传送门有四个标有整数 $ 0,1,2,3 $ 的面,分别对应北、东、南、西方向。当激光以速度 $ x_\text{in} $ 进入传送门 $ (i, j) $ 的面 $ k $ 时,它会以速度 $ x_\text{out} = \max(x_\text{in},s_{i,j}) $ 从面 $ (k+2+t_{i,j}) \bmod 4 $ 离开。传送门消耗的能量为 $ x_\text{out} - x_\text{in} $。
Pak Chanek会射出 $ 4nm $ 道初始速度为 $ 1 $ 的激光,每道激光最终会离开网格或通过 $ 10^{100} $ 个传送门。
最后,如果传送门消耗的总能量模 $ 2 $ 等于其类型,则称该传送门为好传送门。给定所有传送门的强度设置,找到一种分配传送门类型设置的方法,以最大化好传送门的数量。
**输入输出格式**:
**输入格式**:
第一行包含两个整数 $ n $ 和 $ m $($ 1 \le n, m \le 1000 $)——网格的行数和列数。
接下来的 $ n $ 行中的第 $ i $ 行包含 $ m $ 个整数,第 $ j $ 个整数为 $ s_{i,j} $($ 1 \leq s_{i,j} \leq 10^9 $)——传送门 $ (i, j) $ 的强度。
**输出格式**:
输出 $ n $ 行,每行包含一个长度为 $ m $ 的字符串,由字符 $ 0 $ 或 $ 1 $ 组成,表示传送门的类型设置。第 $ i $ 行的第 $ j $ 个字符是传送门 $ (i, j) $ 的类型设置。
如果有多个解决方案,您可以输出其中任何一个。
**输入输出样例**:
**输入样例 #1**:
```
2 3
8 8 2
6 5 7
```
**输出样例 #1**:
```
110
100
```
**输入样例 #2**:
```
1 2
420 69
```
**输出样例 #2**:
```
10
```
**说明**:
在第一个例子中,考虑Pak Chanek射入传送门 $ (2, 2) $ 面积 $ 1 $ 的激光。激光的传播如下:
1. 激光以速度 $ 1 $ 进入传送门 $ (2, 2) $ 的面 $ 1 $。它以速度 $ 5 $ 从面 $ 3 $ 离开。传送门 $ (2, 2) $ 消耗 $ 4 $ 单位的能量。
2. 激光以速度 $ 5 $ 进入传送门 $ (2, 1) $ 的面 $ 1 $。它以速度 $ 6 $ 从面 $ 0 $ 离开。传送门 $ (2, 1) $ 消耗 $ 1 $ 单位的能量。
3. 激光以速度 $ 6 $ 进入传送门 $ (1, 1) $ 的面 $ 2 $。它以速度 $ 8 $ 从面 $ 1 $ 离开。传送门 $ (1, 1) $ 消耗 $ 2 $ 单位的能量。
4. 激光以速度 $ 8 $ 进入传送门 $ (1, 2) $ 的面 $ 3**危险激光功率** **题意翻译**: 有一个 $ n \times m(n,m \leq 1000) $ 的矩阵 $ a $,每个格子分配一个01变量 $ t_{i,j} $。从某个格子的某个边界射入一道激光,维护初始是 $ 1 $ 的前缀最大值,进入一个格子的时候chkmax,把增量计入这个格子的贡献。如果 $ t_{i,j} = 1 $ 则右转,否则直行。激光遇到环或者离开矩阵的时候消失。对所有 $ 4nm $ 种选起点的方式求出每个格子的贡献和。如果这个数和 $ t_{i,j} $ 奇偶性相同则称这是一个好格子。最大化好格子的数量。 **题目描述**: Pak Chanek有一个 $ n \times m $ 的传送门网格。传送门 $ (i,j) $ 有以下设置: - 类型 $ t_{i,j} $,值为 $ 0 $ 或 $ 1 $。 - 强度 $ s_{i,j} $,为 $ 1 $ 到 $ 10^9 $ 之间的整数。 每个传送门有四个标有整数 $ 0,1,2,3 $ 的面,分别对应北、东、南、西方向。当激光以速度 $ x_\text{in} $ 进入传送门 $ (i, j) $ 的面 $ k $ 时,它会以速度 $ x_\text{out} = \max(x_\text{in},s_{i,j}) $ 从面 $ (k+2+t_{i,j}) \bmod 4 $ 离开。传送门消耗的能量为 $ x_\text{out} - x_\text{in} $。 Pak Chanek会射出 $ 4nm $ 道初始速度为 $ 1 $ 的激光,每道激光最终会离开网格或通过 $ 10^{100} $ 个传送门。 最后,如果传送门消耗的总能量模 $ 2 $ 等于其类型,则称该传送门为好传送门。给定所有传送门的强度设置,找到一种分配传送门类型设置的方法,以最大化好传送门的数量。 **输入输出格式**: **输入格式**: 第一行包含两个整数 $ n $ 和 $ m $($ 1 \le n, m \le 1000 $)——网格的行数和列数。 接下来的 $ n $ 行中的第 $ i $ 行包含 $ m $ 个整数,第 $ j $ 个整数为 $ s_{i,j} $($ 1 \leq s_{i,j} \leq 10^9 $)——传送门 $ (i, j) $ 的强度。 **输出格式**: 输出 $ n $ 行,每行包含一个长度为 $ m $ 的字符串,由字符 $ 0 $ 或 $ 1 $ 组成,表示传送门的类型设置。第 $ i $ 行的第 $ j $ 个字符是传送门 $ (i, j) $ 的类型设置。 如果有多个解决方案,您可以输出其中任何一个。 **输入输出样例**: **输入样例 #1**: ``` 2 3 8 8 2 6 5 7 ``` **输出样例 #1**: ``` 110 100 ``` **输入样例 #2**: ``` 1 2 420 69 ``` **输出样例 #2**: ``` 10 ``` **说明**: 在第一个例子中,考虑Pak Chanek射入传送门 $ (2, 2) $ 面积 $ 1 $ 的激光。激光的传播如下: 1. 激光以速度 $ 1 $ 进入传送门 $ (2, 2) $ 的面 $ 1 $。它以速度 $ 5 $ 从面 $ 3 $ 离开。传送门 $ (2, 2) $ 消耗 $ 4 $ 单位的能量。 2. 激光以速度 $ 5 $ 进入传送门 $ (2, 1) $ 的面 $ 1 $。它以速度 $ 6 $ 从面 $ 0 $ 离开。传送门 $ (2, 1) $ 消耗 $ 1 $ 单位的能量。 3. 激光以速度 $ 6 $ 进入传送门 $ (1, 1) $ 的面 $ 2 $。它以速度 $ 8 $ 从面 $ 1 $ 离开。传送门 $ (1, 1) $ 消耗 $ 2 $ 单位的能量。 4. 激光以速度 $ 8 $ 进入传送门 $ (1, 2) $ 的面 $ 3