MEX Tree Manipulation

题意翻译

### 题目描述 定义一棵树上每个节点的值为其所有儿子的值的 MEX，叶子节点的值为 $0$。 现在有一个初始只有节点 $1$ 的树，每次输入一个 $x_i$ 代表加入一个点 $i+1$，它的父亲为 $x_i$，求加入这个点之后树上所有点的权值和。 ### 输入描述 第一行一个数 $q$，接下来接下来 $q$ 行每行一个数 $x_i$。 ### 输出描述 输出 $q$ 行，每行一个数，代表加入点 $i+1$ 后所有点的值的和。 ### 数据范围 $1\leq q\le 3\times 10 ^ 5$，$1\le x_i\le i$。

题目描述

Given a rooted tree, define the value of vertex $ u $ in the tree recursively as the MEX $ ^\dagger $ of the values of its children. Note that it is only the children, not all of its descendants. In particular, the value of a leaf is $ 0 $ . Pak Chanek has a rooted tree that initially only contains a single vertex with index $ 1 $ , which is the root. Pak Chanek is going to do $ q $ queries. In the $ i $ -th query, Pak Chanek is given an integer $ x_i $ . Pak Chanek needs to add a new vertex with index $ i+1 $ as the child of vertex $ x_i $ . After adding the new vertex, Pak Chanek needs to recalculate the values of all vertices and report the sum of the values of all vertices in the current tree. $ ^\dagger $ The MEX (minimum excluded) of an array is the smallest non-negative integer that does not belong to the array. For example, the MEX of $ [0,1,1,2,6,7] $ is $ 3 $ and the MEX of $ [6,9] $ is $ 0 $ .

输入输出格式

输入格式

The first line contains a single integer $ q $ ( $ 1 \le q \le 3 \cdot 10^5 $ ) — the number of operations. Each of the next $ q $ lines contains a single integer $ x_i $ ( $ 1 \leq x_i \leq i $ ) — the description of the $ i $ -th query.

输出格式

For each query, print a line containing an integer representing the sum of the new values of all vertices in the tree after adding the vertex.

输入输出样例

输入样例 #1

7
1
1
3
2
5
2
1

输出样例 #1

1
1
3
2
4
4
7

输入样例 #2

8
1
1
1
1
5
6
7
8

输出样例 #2

1
1
1
1
3
2
4
3

说明

In the first example, the tree after the $ 6 $ -th query will look like this. 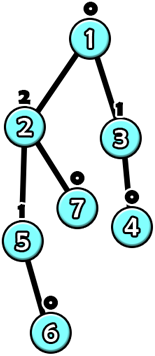 - Vertex $ 7 $ is a leaf, so its value is $ 0 $ . - Vertex $ 6 $ is a leaf, so its value is $ 0 $ . - Vertex $ 5 $ only has a child with value $ 0 $ , so its value is $ 1 $ . - Vertex $ 4 $ is a leaf, so its value is $ 0 $ . - Vertex $ 3 $ only has a child with value $ 0 $ , so its value is $ 1 $ . - Vertex $ 2 $ has children with values $ 0 $ and $ 1 $ , so its value is $ 2 $ . - Vertex $ 1 $ has children with values $ 1 $ and $ 2 $ , so its value is $ 0 $ . The sum of the values of all vertices is $ 0+0+1+0+1+2+0=4 $ .

题目描述：
定义一棵树上每个节点的值为其所有儿子的值的 MEX，叶子节点的值为 $0$。

现在有一个初始只有节点 $1$ 的树，每次输入一个 $x_i$ 代表加入一个点 $i+1$，它的父亲为 $x_i$，求加入这个点之后树上所有点的权值和。

输入描述：
第一行一个数 $q$，接下来 $q$ 行每行一个数 $x_i$。

输出描述：
输出 $q$ 行，每行一个数，代表加入点 $i+1$ 后所有点的值的和。

数据范围：
$1\leq q\le 3\times 10 ^ 5$，$1\le x_i\le i$。

输入输出格式：
输入格式：
第一行包含一个整数 $ q $ ($ 1 \le q \le 3 \times 10^5 $) —— 操作的次数。
接下来 $ q $ 行，每行包含一个整数 $ x_i $ ($ 1 \leq x_i \leq i $) —— 第 $ i $ 次操作的描述。

输出格式：
对于每次操作，打印一行包含一个整数，表示在添加顶点后树中所有顶点的新值的总和。题目描述： 定义一棵树上每个节点的值为其所有儿子的值的 MEX，叶子节点的值为 $0$。 现在有一个初始只有节点 $1$ 的树，每次输入一个 $x_i$ 代表加入一个点 $i+1$，它的父亲为 $x_i$，求加入这个点之后树上所有点的权值和。 输入描述： 第一行一个数 $q$，接下来 $q$ 行每行一个数 $x_i$。 输出描述： 输出 $q$ 行，每行一个数，代表加入点 $i+1$ 后所有点的值的和。 数据范围： $1\leq q\le 3\times 10 ^ 5$，$1\le x_i\le i$。 输入输出格式： 输入格式： 第一行包含一个整数 $ q $ ($ 1 \le q \le 3 \times 10^5 $) —— 操作的次数。 接下来 $ q $ 行，每行包含一个整数 $ x_i $ ($ 1 \leq x_i \leq i $) —— 第 $ i $ 次操作的描述。 输出格式： 对于每次操作，打印一行包含一个整数，表示在添加顶点后树中所有顶点的新值的总和。