407521: GYM102822 B Building Blocks
Description
As we know, for a three-dimensional object, we can draw its three views — front view, top view, and left view. We can regard these views as the projections of the object onto different planes.
For example, consider some blocks like this:

The three views can be drawn as follows:

But Little Rabbit thinks these views are too boring. He wants to observe these blocks in a quite special view — left-front view. Still consider the blocks given above. The left-front view can be drawn as follow:
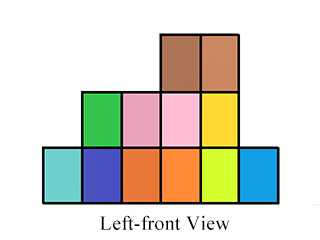
The left-front view can also be regarded as a projection onto a plane, while the plane is at an angle of $$$45^\circ$$$ to the left view's plane and the front view's plane. The following picture shows how it projects in a top view.

Therefore, if we regard the top view as a grid with $$$n$$$ rows and $$$m$$$ columns, the left-front view should have $$$n+m$$$ columns.
Now, Little Rabbit wants to build some blocks to meet the following conditions:
- The top view is a grid with $$$n$$$ rows and $$$m$$$ columns. Each square should place at least one block.
- Each column of the left-front view has a height of $$$a_1,a_2,\dots,a_{n+m}$$$ from left to right.
- The $$$x_i$$$-th row and the $$$y_i$$$-th column of the top view has exactly $$$h_i$$$ blocks. There are $$$k$$$ such conditions.
Little Rabbit wonders how many different methods there are to meet all the conditions. Since the answer can be very large, please tell him the answer modulo $$$10^9+7$$$.
InputThe first line of the input contains an integer $$$T$$$ ($$$1 \le T \le 10^5$$$) — the number of test cases.
The first line of each test case contains three integers $$$n,m,k$$$ ($$$1 \le n,m,k \le 10^5$$$) — the number of rows and columns of the top view, and the number of conditions. The sum of $$$n$$$, the sum of $$$m$$$, and the sum of $$$k$$$ will not exceed $$$10^5$$$.
The second line contains $$$n+m$$$ integers $$$a_1,a_2,\dots,a_{n+m}$$$ ($$$1 \le a_1,a_2,\dots,a_{n+m} \le 10^9$$$) — the heights of the left-front view from left to right.
Then in the next $$$k$$$ lines, the $$$i$$$-th line contains three integers $$$x_i,y_i,h_i$$$ ($$$1 \le x_i \le n$$$, $$$1 \le y_i \le m$$$, $$$1 \le h_i \le 10^9$$$), which means the $$$x_i$$$-th row and the $$$y_i$$$-th column of the top view has exactly $$$h_i$$$ blocks. It's guaranteed that all $$$(x_i,y_i)$$$ are distinct.
OutputFor the $$$x$$$-th test case, if the answer modulo $$$10^9+7$$$ is $$$y$$$, output $$$Case$$$ #$$$x$$$: $$$y$$$ in a single line.
ExampleInput2 3 3 1 1 2 2 3 3 1 2 3 3 2 2 1 2 2 2 2 1 2 2Output
Case #1: 72 Case #2: 2