405957: GYM102191 H Convex Polygons
Description
You are given a string of digits from 1 to 8, each digit represents one of the 8 directions in clockwise order as shown in the following picture. The picture also states the changes in the X and Y coordinates for each direction.
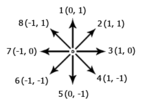
Count the number of substrings such that if you start at (0, 0) and follow the directional moves in the substring, you will draw one closed convex polygon, that is, you need to finish at (0, 0), all interior angles should be less than or equal to 180°, and the polygon should not intersect itself.
InputThe first line of input contains a single integer n (1 ≤ n ≤ 3 × 105), the length of the string.
The second line contains a string of n digits from 1 to 8.
OutputOutput on a single line with the number of substrings that draw out one closed convex polygon.
ExamplesInput8 31753317Output
3Input
8 33228666Output
1Input
8 28863535Output
0Note
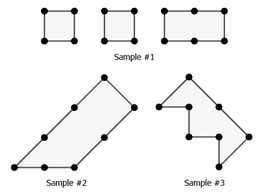
In the first sample test, substrings (1, 4), (2, 5), and (3, 6) draws the three convex polygons from left to right, respectively.
In the second sample test, the whole string represents a convex polygon, any other substring will be open, so the answer is 1.
In the third sample test, the whole string represents a closed polygon but it is not convex, other substrings draw open polygons, so the answer is 0.