311334: CF1970G2. Min-Fund Prison (Medium)

G2. Min-Fund Prison (Medium)time limit per test1.5 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

In the medium version, $2 \leq \sum n \leq 300$ and $1 \leq \sum m \leq 300$

After a worker's strike organized by the Dementors asking for equal rights, the prison of Azkaban has suffered some damage. After settling the spirits, the Ministry of Magic is looking to renovate the prison to ensure that the Dementors are kept in check. The prison consists of $n$ prison cells and $m$ bi-directional corridors. The $i^{th}$ corridor is from cells $u_i$ to $v_i$. A subset of these cells $S$ is called a complex if any cell in $S$ is reachable from any other cell in $S$. Formally, a subset of cells $S$ is a complex if $x$ and $y$ are reachable from each other for all $x, y \in S$, using only cells from $S$ on the way. The funding required for a complex $S$ consisting of $k$ cells is defined as $k^2$.

As part of your Intro to Magical Interior Design course at Hogwarts, you have been tasked with designing the prison. The Ministry of Magic has asked that you divide the prison into $2$ complexes with $\textbf{exactly one corridor}$ connecting them, so that the Dementors can't organize union meetings. For this purpose, you are allowed to build bi-directional corridors. The funding required to build a corridor between any $2$ cells is $c$.

Due to budget cuts and the ongoing fight against the Death Eaters, you must find the $\textbf{minimum total funding}$ required to divide the prison as per the Ministry's requirements or $-1$ if no division is possible.

Note: The total funding is the sum of the funding required for the $2$ complexes and the corridors built. If after the division, the two complexes have $x$ and $y$ cells respectively and you have built a total of $a$ corridors, the total funding will be $x^2 + y^2 + c \times a$. Note that $x+y=n$.

Input

The first line contains one integer $t$ ($1 \leq t \leq 300$) — the number of test cases. Then $t$ test cases follow.

The first line of each test case consists of three integers $n, m$ and $c$ ($2 \leq n \leq 300$, $1 \leq m \leq 300$, $1 \leq c \leq 10^9$)

$m$ lines follow, each consisting of 2 integers — $u_i, v_i$ indicating a corridor is present between cells $u_i$ and $v_i$ ($1 \leq u_i, v_i \leq n$, $u_i \neq v_i$)

It is guaranteed that the sum of $n$ over all test cases does not exceed $300$.

It is guaranteed that the sum of $m$ over all test cases does not exceed $300$.

It is guaranteed that there exists at most one corridor between any two cells.

Output

Print the $\textbf{minimum funding}$ required to divide the prison as per the Ministry's requirements or $-1$ if no division is possible.

ExampleInput

4
4 6 5
4 3
2 3
2 4
1 2
4 1
3 1
6 6 2
1 4
2 5
3 6
1 5
3 5
6 5
6 5 7
1 4
2 5
3 6
3 5
6 5
7 5 4
1 4
3 6
3 5
6 5
2 7

Output

-1
20
25
33

Note

In the first test case of the sample input, there is no way to divide the prison according to the Ministry's requirements.

In the second test case, consider the corridor between cells $1$ and $5$ as the connection between the $2$ complexes consisting of $\{2, 3, 5, 6\}$ and $\{1, 4\}$ cells respectively. There are no new corridors built. The total funding is $4^2 + 2^2 = 20$. You can verify this is the minimum funding required.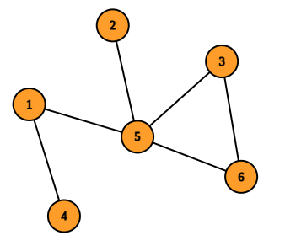

In the third test case, build a corridor between $2$ and $4$. Consider the corridor between cells $1$ and $5$ as the connection between the $2$ complexes consisting of $\{3, 5, 6\}$ and $\{1, 2, 4\}$ cells respectively. The total funding is $3^2 + 3^2 + 7 \times 1 = 25$. You can verify this is the minimum funding required.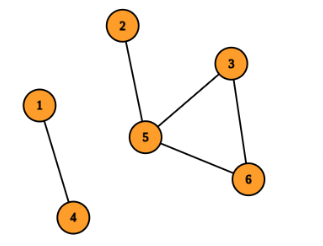

In the fourth test case, build a corridor between $2$ and $4$ and between $5$ and $7$. Consider the corridor between cells $5$ and $7$ as the connection between the $2$ complexes consisting of $\{1, 2, 4, 7\}$ and $\{3, 5, 6\}$ cells respectively. The total funding is $4^2 + 3^2 + 4 \times 2 = 33$. You can verify this is the minimum funding required.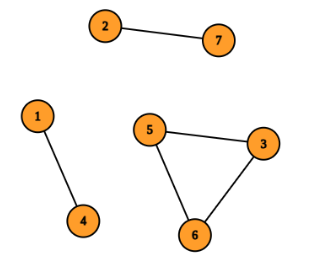

Note for all test cases that there may be multiple ways to get the same funding but there is no other division which will have a more optimal minimum funding.

题目大意：给定一个监狱，由n个牢房和m条双向走廊组成。每条走廊连接两个牢房。如果一组牢房S中的任意两个牢房x和y都互相可达，则称S为一个复杂。对于每个复杂S，其所需资金为k^2，其中k为S中的牢房数量。现要将监狱划分为两个复杂，这两个复杂之间恰好有一条走廊连接，且要使所需资金最小。如果无法满足要求，则输出-1。

输入数据格式：第一行包含一个整数t，表示测试用例的数量。接下来t个测试用例，每个测试用例的第一行包含三个整数n、m和c，分别表示牢房的数量、走廊的数量和建立一条走廊所需的资金。接下来m行，每行包含两个整数u_i和v_i，表示牢房u_i和牢房v_i之间有一条走廊。保证所有测试用例的n之和不超过300，m之和不超过300，且任意两个牢房之间最多有一条走廊。

输出数据格式：对于每个测试用例，输出划分监狱所需的最小资金，如果无法满足要求，则输出-1。题目大意：给定一个监狱，由n个牢房和m条双向走廊组成。每条走廊连接两个牢房。如果一组牢房S中的任意两个牢房x和y都互相可达，则称S为一个复杂。对于每个复杂S，其所需资金为k^2，其中k为S中的牢房数量。现要将监狱划分为两个复杂，这两个复杂之间恰好有一条走廊连接，且要使所需资金最小。如果无法满足要求，则输出-1。 输入数据格式：第一行包含一个整数t，表示测试用例的数量。接下来t个测试用例，每个测试用例的第一行包含三个整数n、m和c，分别表示牢房的数量、走廊的数量和建立一条走廊所需的资金。接下来m行，每行包含两个整数u_i和v_i，表示牢房u_i和牢房v_i之间有一条走廊。保证所有测试用例的n之和不超过300，m之和不超过300，且任意两个牢房之间最多有一条走廊。 输出数据格式：对于每个测试用例，输出划分监狱所需的最小资金，如果无法满足要求，则输出-1。