310978: CF1916E. Happy Life in University
Description
Egor and his friend Arseniy are finishing school this year and will soon enter university. And since they are very responsible guys, they have started preparing for admission already.
First of all, they decided to take care of where they will live for the long four years of study, and after visiting the university's website, they found out that the university dormitory can be represented as a root tree with $n$ vertices with the root at vertex $1$. In the tree, each vertex represents a recreation with some type of activity $a_i$. The friends need to choose $2$ recreations (not necessarily different) in which they will settle. The guys are convinced that the more the value of the following function $f(u, v) = diff(u, lca(u, v)) \cdot diff(v, lca(u, v))$, the more fun their life will be. Help Egor and Arseniy and find the maximum value of $f(u, v)$ among all pairs of recreations!
$^{\dagger} diff(u, v)$ — the number of different activities listed on the simple path from vertex $u$ to vertex $v$.
$^{\dagger} lca(u, v)$ — a vertex $p$ such that it is at the maximum distance from the root and is a parent of both vertex $u$ and vertex $v$.
InputEach test consists of several test cases. The first line contains a single integer $t$ ($1 \le t \le 10^5$) — the number of test cases. Then follows the description of the test cases.
The first line of each test case contains a single integer $n$ ($1 \le n \le 3 \cdot 10^{5}$).
The second line of each test case contains ${n - 1}$ integers $p_2, p_3, \ldots,p_n$ ($1 \le p_i \le i - 1$), where $p_i$ — the parent of vertex $i$.
The third line of each test case contains ${n}$ integers $a_1, a_2, \ldots,a_n$ ($1 \le a_i \le n$), where $a_i$ — the number of the activity located at vertex $i$.
It is guaranteed that the sum of $n$ over all test cases does not exceed $3 \cdot 10^5$.
OutputFor each test case, output the maximum value of $f(u, v)$ for all pairs of recreations $(u, v)$.
ExampleInput4 2 1 1 2 7 1 1 2 2 3 3 6 5 2 3 6 5 6 13 1 1 1 2 2 2 3 3 4 5 6 6 2 2 2 1 4 9 7 2 5 2 1 11 2 12 1 1 1 2 2 3 4 4 7 7 6 11 2 1 11 12 8 5 8 8 5 11 7Output
2 9 9 12Note
Consider the fourth test case. The tree has the following structure:
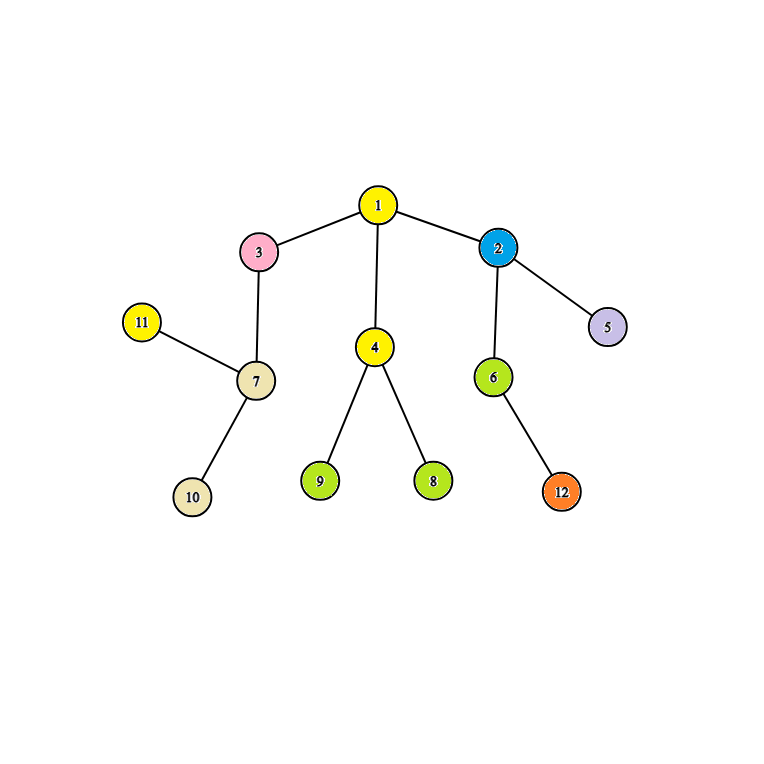
Output
Egor和他的朋友Arseniy即将完成中学学业并进入大学。他们首先决定解决未来四年学习期间的住宿问题。通过访问大学网站,他们发现学生宿舍可以表示为一个有n个顶点的树,根顶点为1。树中的每个顶点代表一种活动ai。朋友们需要选择两个娱乐场所(不一定是不同的)来定居。他们认为,f(u, v)的值越大,他们的生活就越有趣。你的任务是帮助Egor和Arseniy找到所有娱乐场所对中f(u, v)的最大值。
f(u, v) = diff(u, lca(u, v)) * diff(v, lca(u, v))
diff(u, v)是从顶点u到顶点v的简单路径上列出的不同活动的数量。
lca(u, v)是一个顶点p,它离根最远,并且是顶点u和顶点v的父顶点。
输入输出数据格式:
输入:
每个测试包含多个测试用例。第一行包含一个整数t(1≤t≤10^5)——测试用例的数量。然后是测试用例的描述。
每个测试用例的第一行包含一个整数n(1≤n≤3*10^5)。
每个测试用例的第二行包含n-1个整数p2, p3, ..., pn(1≤pi≤i-1),其中pi是顶点i的父顶点。
每个测试用例的第三行包含n个整数a1, a2, ..., an(1≤ai≤n),其中ai是位于顶点i的活动编号。
保证所有测试用例的n之和不超过3*10^5。
输出:
对于每个测试用例,输出所有娱乐场所对(u, v)的f(u, v)的最大值。题目大意: Egor和他的朋友Arseniy即将完成中学学业并进入大学。他们首先决定解决未来四年学习期间的住宿问题。通过访问大学网站,他们发现学生宿舍可以表示为一个有n个顶点的树,根顶点为1。树中的每个顶点代表一种活动ai。朋友们需要选择两个娱乐场所(不一定是不同的)来定居。他们认为,f(u, v)的值越大,他们的生活就越有趣。你的任务是帮助Egor和Arseniy找到所有娱乐场所对中f(u, v)的最大值。 f(u, v) = diff(u, lca(u, v)) * diff(v, lca(u, v)) diff(u, v)是从顶点u到顶点v的简单路径上列出的不同活动的数量。 lca(u, v)是一个顶点p,它离根最远,并且是顶点u和顶点v的父顶点。 输入输出数据格式: 输入: 每个测试包含多个测试用例。第一行包含一个整数t(1≤t≤10^5)——测试用例的数量。然后是测试用例的描述。 每个测试用例的第一行包含一个整数n(1≤n≤3*10^5)。 每个测试用例的第二行包含n-1个整数p2, p3, ..., pn(1≤pi≤i-1),其中pi是顶点i的父顶点。 每个测试用例的第三行包含n个整数a1, a2, ..., an(1≤ai≤n),其中ai是位于顶点i的活动编号。 保证所有测试用例的n之和不超过3*10^5。 输出: 对于每个测试用例,输出所有娱乐场所对(u, v)的f(u, v)的最大值。