310652: CF1866C. Completely Searching for Inversions

C. Completely Searching for Inversionstime limit per test2 secondsmemory limit per test512 megabytesinputstandard inputoutputstandard output

Pak Chanek has a directed acyclic graph (a directed graph that does not have any cycles) containing $N$ vertices. Vertex $i$ has $S_i$ edges directed away from that vertex. The $j$-th edge of vertex $i$ that is directed away from it, is directed towards vertex $L_{i,j}$ and has an integer $W_{i,j}$ ($0\leq W_{i,j}\leq1$). Another information about the graph is that the graph is shaped in such a way such that each vertex can be reached from vertex $1$ via zero or more directed edges.

Pak Chanek has an array $Z$ that is initially empty.

Pak Chanek defines the function dfs as follows:

// dfs from vertex i
void dfs(int i) {
    // iterate each edge of vertex i that is directed away from it
    for(int j = 1; j <= S[i]; j++) {
        Z.push_back(W[i][j]); // add the integer in the edge to the end of Z
        dfs(L[i][j]); // recurse to the next vertex
    }
}

Note that the function does not keep track of which vertices have been visited, so each vertex can be processed more than once.

Let's say Pak Chanek does dfs(1) once. After that, Pak Chanek will get an array $Z$ containing some elements $0$ or $1$. Define an inversion in array $Z$ as a pair of indices $(x, y)$ ($x < y$) such that $Z_x > Z_y$. How many different inversions in $Z$ are there if Pak Chanek does dfs(1) once? Since the answer can be very big, output the answer modulo $998\,244\,353$.

Input

The first line contains a single integer $N$ ($2 \leq N \leq 10^5$) — the number of vertices in the graph. The following lines contain the description of each vertex from vertex $1$ to vertex $N$.

The first line of each vertex $i$ contains a single integer $S_i$ ($0 \leq S_i \leq N-1$) — the number of edges directed away from vertex $i$.

The $j$-th of the next $S_i$ lines of each vertex $i$ contains two integers $L_{i,j}$ and $W_{i,j}$ ($1 \leq L_{i,j} \leq N$; $0 \leq W_{i,j} \leq 1$) — an edge directed away from vertex $i$ that is directed towards vertex $L_{i,j}$ and has an integer $W_{i,j}$. For each $i$, the values of $L_{i,1}$, $L_{i,2}$, ..., $L_{i,S_i}$ are pairwise distinct.

It is guaranteed that the sum of $S_i$ over all vertices does not exceed $2 \cdot 10^5$. There are no cycles in the graph. Each vertex can be reached from vertex $1$ via zero or more directed edges.

Output

An integer representing the number of inversions in $Z$ if Pak Chanek does dfs(1) once. Since the answer can be very big, output the answer modulo $998\,244\,353$.

ExampleInput

5
2
4 0
3 1
0
1
2 0
2
3 1
5 1
0

Output

4

Note

The following is the dfs(1) process on the graph.

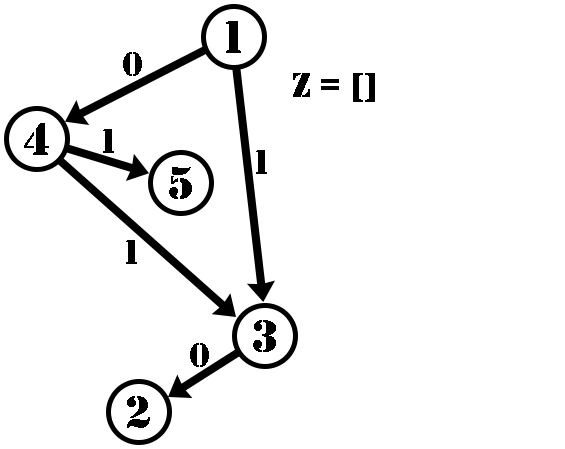
In the end, $Z=[0,1,0,1,1,0]$. All of its inversions are $(2,3)$, $(2,6)$, $(4,6)$, and $(5,6)$.

题目大意：
Pak Chanek有一个包含N个顶点的有向无环图（一个没有环的有向图）。顶点i有Si条边从该顶点出发。顶点i的第j条边有一个整数Wi,j（0≤Wi,j≤1）。关于图的其他信息是，图的结构使得每个顶点都可以通过零或多条有向边从顶点1到达。Pak Chanek有一个初始为空的数组Z。Pak Chanek定义了函数dfs如下：

输入输出数据格式：
输入：
第一行包含一个整数N（2≤N≤10^5）——图中顶点的数量。接下来的行包含从顶点1到顶点N的每个顶点的描述。
每个顶点i的第一行包含一个整数Si（0≤Si≤N-1）——从顶点i出发的边的数量。
每个顶点i的接下来的Si行包含两个整数Li,j和Wi,j（1≤Li,j≤N；0≤Wi,j≤1）——一条从顶点i出发并指向顶点Li,j的边，以及该边的整数Wi,j。对于每个i，Li,1，Li,2，...，Li,Si的值是两两不同的。
保证所有顶点的Si之和不超过2×10^5。图中没有环。每个顶点都可以通过零或多条有向边从顶点1到达。

输出：
如果Pak Chanek执行一次dfs(1)，则输出数组Z中的逆序数。由于答案可能非常大，请将答案模998244353后输出。题目大意： Pak Chanek有一个包含N个顶点的有向无环图（一个没有环的有向图）。顶点i有Si条边从该顶点出发。顶点i的第j条边有一个整数Wi,j（0≤Wi,j≤1）。关于图的其他信息是，图的结构使得每个顶点都可以通过零或多条有向边从顶点1到达。Pak Chanek有一个初始为空的数组Z。Pak Chanek定义了函数dfs如下： 输入输出数据格式： 输入： 第一行包含一个整数N（2≤N≤10^5）——图中顶点的数量。接下来的行包含从顶点1到顶点N的每个顶点的描述。 每个顶点i的第一行包含一个整数Si（0≤Si≤N-1）——从顶点i出发的边的数量。 每个顶点i的接下来的Si行包含两个整数Li,j和Wi,j（1≤Li,j≤N；0≤Wi,j≤1）——一条从顶点i出发并指向顶点Li,j的边，以及该边的整数Wi,j。对于每个i，Li,1，Li,2，...，Li,Si的值是两两不同的。 保证所有顶点的Si之和不超过2×10^5。图中没有环。每个顶点都可以通过零或多条有向边从顶点1到达。 输出： 如果Pak Chanek执行一次dfs(1)，则输出数组Z中的逆序数。由于答案可能非常大，请将答案模998244353后输出。