310610: CF1859D. Andrey and Escape from Capygrad

D. Andrey and Escape from Capygradtime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

An incident occurred in Capygrad, the capital of Tyagoland, where all the capybaras in the city went crazy and started throwing mandarins. Andrey was forced to escape from the city as far as possible, using portals.

Tyagoland is represented by a number line, and the city of Capygrad is located at point $0$. There are $n$ portals all over Tyagoland, each of which is characterised by four integers $l_i$, $r_i$, $a_i$ and $b_i$ ($1 \le l_i \le a_i \le b_i \le r_i \le 10^9$). Note that the segment $[a_i, b_i]$ is contained in the segment $[l_i, r_i]$.

If Andrey is on the segment $[l_i, r_i]$, then the portal can teleport him to any point on the segment $[a_i, b_i]$. Andrey has a pass that allows him to use the portals an unlimited number of times.

Andrey thinks that the point $x$ is on the segment $[l, r]$ if the inequality $l \le x \le r$ is satisfied.

Andrey has $q$ options for where to start his escape, each option is characterized by a single integer $x_i$ — the starting position of the escape. He wants to escape from Capygrad as far as possible (to the point with the maximum possible coordinate). Help Andrey determine how far he could escape from Capygrad, starting at each of the $q$ positions.

Input

Each test consists of multiple test cases. The first line contains a single integer $t$ ($1 \le t \le 10^4$) — the number of sets of test cases. The description of test cases follows.

The first line of each test case contains a single integer $n$ ($1 \le n \le 2 \cdot 10^5$) — the number of portals.

Each of the next $n$ lines contains four integers $l_i$, $r_i$, $a_i$, and $b_i$ $(1 \le l_i \le a_i \le b_i \le r_i \le 10^9)$ — the characteristics of the portals.

The next line contains a single integer $q$ ($1 \le q \le 2 \cdot 10^5$) — the number of positions.

The following line contains $q$ integers $x_1, x_2, \ldots, x_q$ ($1 \le x_i \le 10^9$) — the position from which Andrey will start his escape in the $i$-th options.

It is guaranteed that the sum of $n$ and the sum of $q$ over all test cases does not exceed $2 \cdot 10^5$.

Output

For each test case, output a single line of $q$ integers, containing the answers to Andrey's questions.

ExampleInput

5
3
6 17 7 14
1 12 3 8
16 24 20 22
6
10 2 23 15 28 18
3
3 14 7 10
16 24 20 22
1 16 3 14
9
2 4 6 8 18 23 11 13 15
2
1 4 2 3
3 9 6 7
3
4 8 1
5
18 24 18 24
1 8 2 4
11 16 14 14
26 32 28 30
5 10 6 8
9
15 14 13 27 22 17 31 1 7
6
9 22 14 20
11 26 13 24
21 33 22 23
21 33 25 32
1 6 3 4
18 29 20 21
8
11 23 16 5 8 33 2 21

Output

14 14 23 15 28 22 
14 14 14 14 22 23 14 14 15 
7 8 7 
15 14 14 30 24 17 31 4 8 
32 32 32 5 8 33 4 32 

Note

In the first test case:

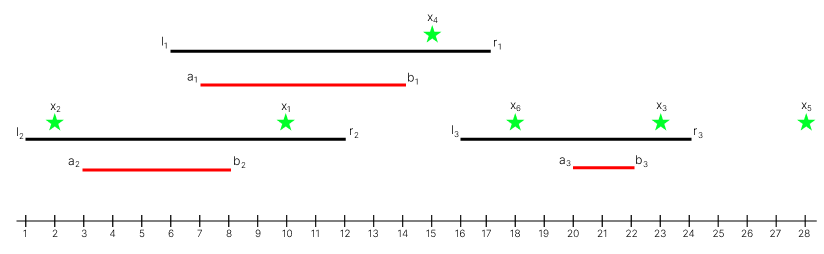
Optimal actions when starting from each position:

1. Use portal $1$ and teleport to point $b_1 = 14$.
2. Use portal $2$ first and teleport to point $6$, which is on the segment $[l_1, r_1] = [6, 17]$, then use portal $1$ and teleport to point $b_1 = 14$.
3. Stay at point $x_3=23$ without using any portals.
4. Stay at point $x_4=15$ without using any portals.
5. Point $x_5=28$ is not on any segment, so Andrey won't be able to teleport anywhere.
6. Point $x_6=18$ is only on the segment $[l_3, r_3] = [16, 24]$, use portal $3$ and teleport to point $b_3 = 22$.

In the fifth test case:

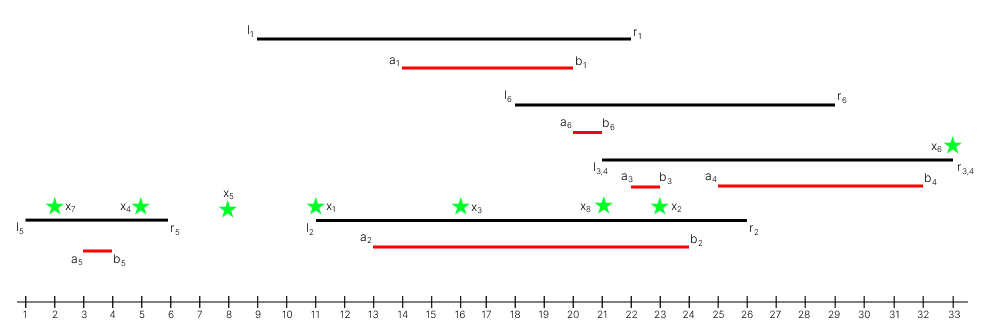
Optimal actions when starting from each position:

1. Use portal $1$ first and teleport to point $15$ on the segment $[a_1, b_1] = [14, 20]$, then use portal $2$ and teleport to point $21$, which is on the segment $[l_4, r_4] = [21, 33]$ and on the segment $[a_2, b_2] = [13, 24]$, then teleport to point $b_4 = 32$.
2. Use portal $6$ first and teleport to point $20$ on the segment $[a_6, b_6] = [20, 21]$, then use portal $2$ and teleport to point $22$, which is simultaneously on the segment $[l_4, r_4] = [21, 33]$ and on the segment $[a_2, b_2] = [13, 24]$, then teleport to point $b_4 = 32$.
3. Perform the same actions as from the first position.
4. Stay at point $x_4=5$ without using any portals.
5. Point $8$ is not on any segment, so Andrey won't be able to teleport anywhere.
6. Stay at point $x_6=33$ without using any portals.
7. Use portal $5$ and teleport to point $b_5 = 4$.
8. Perform the same actions as from the first position.

题目大意：
在泰加兰德的首都卡皮格拉德发生了一个事件，所有的水豚都发疯了，开始扔橘子。安德烈被迫尽可能远地使用传送门逃离城市。

泰加兰德由一条数轴表示，卡皮格拉德城市位于点0。整个泰加兰德有n个传送门，每个传送门由四个整数l_i, r_i, a_i, b_i (1≤l_i≤a_i≤b_i≤r_i≤10^9) 特征化。注意，区间[a_i, b_i]被包含在区间[l_i, r_i]内。

如果安德烈在区间[l_i, r_i]上，那么传送门可以将他传送到区间[a_i, b_i]上的任意一点。安德烈有一张通行证，可以无限次使用传送门。

安德烈认为点x在区间[l, r]上，如果满足不等式l≤x≤r。

安德烈有q个开始逃跑的选择，每个选择由一个整数x_i特征化——逃跑的起始位置。他想要从卡皮格拉德尽可能远地逃离（到坐标最大的点）。帮助安德烈确定从每个q个位置开始，他可以逃离卡皮格拉德多远。

输入输出数据格式：
输入：
每个测试包含多个测试用例。第一行包含一个整数t (1≤t≤10^4) —— 测试用例集的数量。接下来是测试用例的描述。

每个测试用例的第一行包含一个整数n (1≤n≤2×10^5) —— 传送门数量。

接下来的n行，每行包含四个整数l_i, r_i, a_i, b_i (1≤l_i≤a_i≤b_i≤r_i≤10^9) —— 传送门特征。

接下来的一行包含一个整数q (1≤q≤2×10^5) —— 位置数量。

接下来的一行包含q个整数x_1, x_2, …, x_q (1≤x_i≤10^9) —— 安德烈在第i个选项的起始逃跑位置。

保证所有测试用例的n和q之和不超过2×10^5。

输出：
对于每个测试用例，输出一行，包含q个整数，为安德烈问题的答案。题目大意： 在泰加兰德的首都卡皮格拉德发生了一个事件，所有的水豚都发疯了，开始扔橘子。安德烈被迫尽可能远地使用传送门逃离城市。 泰加兰德由一条数轴表示，卡皮格拉德城市位于点0。整个泰加兰德有n个传送门，每个传送门由四个整数l_i, r_i, a_i, b_i (1≤l_i≤a_i≤b_i≤r_i≤10^9) 特征化。注意，区间[a_i, b_i]被包含在区间[l_i, r_i]内。 如果安德烈在区间[l_i, r_i]上，那么传送门可以将他传送到区间[a_i, b_i]上的任意一点。安德烈有一张通行证，可以无限次使用传送门。 安德烈认为点x在区间[l, r]上，如果满足不等式l≤x≤r。 安德烈有q个开始逃跑的选择，每个选择由一个整数x_i特征化——逃跑的起始位置。他想要从卡皮格拉德尽可能远地逃离（到坐标最大的点）。帮助安德烈确定从每个q个位置开始，他可以逃离卡皮格拉德多远。 输入输出数据格式： 输入： 每个测试包含多个测试用例。第一行包含一个整数t (1≤t≤10^4) —— 测试用例集的数量。接下来是测试用例的描述。 每个测试用例的第一行包含一个整数n (1≤n≤2×10^5) —— 传送门数量。 接下来的n行，每行包含四个整数l_i, r_i, a_i, b_i (1≤l_i≤a_i≤b_i≤r_i≤10^9) —— 传送门特征。 接下来的一行包含一个整数q (1≤q≤2×10^5) —— 位置数量。 接下来的一行包含q个整数x_1, x_2, …, x_q (1≤x_i≤10^9) —— 安德烈在第i个选项的起始逃跑位置。 保证所有测试用例的n和q之和不超过2×10^5。 输出： 对于每个测试用例，输出一行，包含q个整数，为安德烈问题的答案。