310440: CF1833G. Ksyusha and Chinchilla

G. Ksyusha and Chinchillatime limit per test3 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

Ksyusha has a pet chinchilla, a tree on $n$ vertices and huge scissors. A tree is a connected graph without cycles. During a boring physics lesson Ksyusha thought about how to entertain her pet.

Chinchillas like to play with branches. A branch is a tree of $3$ vertices.

The branch looks like this.

A cut is the removal of some (not yet cut) edge in the tree. Ksyusha has plenty of free time, so she can afford to make enough cuts so that the tree splits into branches. In other words, after several (possibly zero) cuts, each vertex must belong to exactly one branch.

Help Ksyusha choose the edges to be cut or tell that it is impossible.

Input

The first line contains a single integer $t$ ($1 \le t \le 10^4$) — number of testcases.

The first line of each testcase contains a single integer $n$ ($2 \le n \le 2 \cdot 10^5$) — the number of vertices in the tree.

The next $n - 1$ rows of each testcase contain integers $v_i$ and $u_i$ ($1 \le v_i, u_i \le n$) — the numbers of vertices that the $i$-th edge connects.

It is guaranteed that this set of edges forms a tree. It is also guaranteed that the sum of $n$ over all testcases does not exceed $2 \cdot 10^5$.

Output

Print the answer for each testcase.

If the desired way to cut the tree does not exist, print $-1$.

Otherwise, print an integer $k$ — the number of edges to be cut. In the next line, print $k$ different integers $e_i$ ($1 \le e_i < n$) — numbers of the edges to be cut. If $k = 0$, print an empty string instead.

If there are several solutions, you can print any.

ExamplesInput

4
9
1 2
4 3
7 9
5 4
4 6
3 2
8 7
1 7
6
1 2
1 3
4 3
1 5
6 1
6
1 2
3 2
3 4
4 5
6 5
5
1 3
5 3
5 2
3 4

Output

2
2 8 
-1
1
3 
-1

Input

4
2
1 2
3
1 2
3 1
6
1 2
3 1
3 4
3 5
6 1
9
2 6
6 9
9 1
9 7
1 8
7 3
8 5
4 7

Output

-1
0

1
2 
2
4 3 

Note 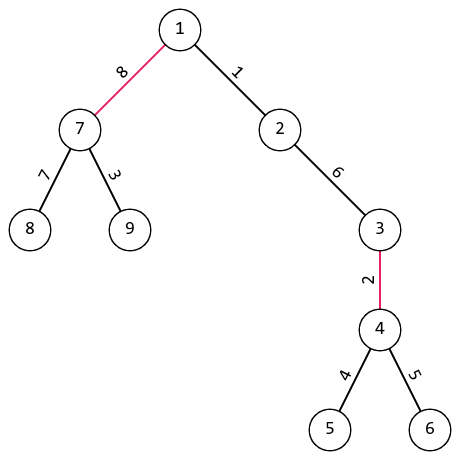The first testcase in first test.

题目大意：
Ksyusha有一只宠物栗鼠和一棵有n个顶点的树，以及一把大剪刀。树是一个没有环的连通图。在无聊的物理课上，Ksyusha想到了如何逗她的宠物。

栗鼠喜欢玩树枝。一个树枝是具有3个顶点的树。

一次切割是指移除树中的一些（尚未切割的）边。Ksyusha有足够的空闲时间，因此她可以进行足够的切割，使树分解成树枝。换句话说，经过几次（可能为零次）切割后，每个顶点必须恰好属于一个树枝。

帮助Ksyusha选择要切割的边，或者告知无法做到。

输入数据格式：
第一行包含一个整数t（1≤t≤10^4）——测试用例的数量。

每个测试用例的第一行包含一个整数n（2≤n≤2×10^5）——树中顶点的数量。

接下来每个测试用例的n-1行包含整数v_i和u_i（1≤v_i,u_i≤n）——第i条边连接的顶点编号。

保证这组边构成一棵树。还保证所有测试用例的n之和不超过2×10^5。

输出数据格式：
为每个测试用例打印答案。

如果不存在所需的切割树的方式，打印-1。

否则，打印一个整数k——要切割的边的数量。在下一行，打印k个不同的整数e_i（1 ≤ e_i < n）——要切割的边的编号。如果k=0，则打印一个空字符串。

如果有多个解决方案，您可以打印任何一个。题目大意： Ksyusha有一只宠物栗鼠和一棵有n个顶点的树，以及一把大剪刀。树是一个没有环的连通图。在无聊的物理课上，Ksyusha想到了如何逗她的宠物。 栗鼠喜欢玩树枝。一个树枝是具有3个顶点的树。 一次切割是指移除树中的一些（尚未切割的）边。Ksyusha有足够的空闲时间，因此她可以进行足够的切割，使树分解成树枝。换句话说，经过几次（可能为零次）切割后，每个顶点必须恰好属于一个树枝。 帮助Ksyusha选择要切割的边，或者告知无法做到。 输入数据格式： 第一行包含一个整数t（1≤t≤10^4）——测试用例的数量。 每个测试用例的第一行包含一个整数n（2≤n≤2×10^5）——树中顶点的数量。 接下来每个测试用例的n-1行包含整数v_i和u_i（1≤v_i,u_i≤n）——第i条边连接的顶点编号。 保证这组边构成一棵树。还保证所有测试用例的n之和不超过2×10^5。 输出数据格式： 为每个测试用例打印答案。 如果不存在所需的切割树的方式，打印-1。 否则，打印一个整数k——要切割的边的数量。在下一行，打印k个不同的整数e_i（1 ≤ e_i < n）——要切割的边的编号。如果k=0，则打印一个空字符串。 如果有多个解决方案，您可以打印任何一个。