310397: CF1827D. Two Centroids
Description
You are given a tree (an undirected connected acyclic graph) which initially only contains vertex $1$. There will be several queries to the given tree. In the $i$-th query, vertex $i + 1$ will appear and be connected to vertex $p_i$ ($1 \le p_i \le i$).
After each query, please find out the least number of operations required to make the current tree has two centroids. In one operation, you can add one vertex and one edge to the tree such that it remains a tree.
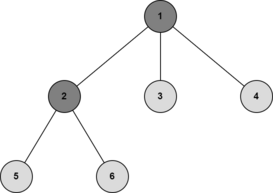
A vertex is called a centroid if its removal splits the tree into subtrees with at most $\lfloor \frac{n}{2} \rfloor$ vertices each, with $n$ as the number of vertices of the tree. For example, the centroid of the following tree is $3$ because the biggest subtree after removing the centroid has $2$ vertices.

In the next tree, vertex $1$ and $2$ are both centroids.
Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \le t \le 10^4$). The description of the test cases follows.
The first line of each test case contains a single integer $n$ ($2 \le n \le 5 \cdot 10^{5}$) — the number of nodes of the final tree.
The second line of each test case contains $n - 1$ integers $p_1, p_2, \ldots, p_{n - 1}$ ($1 \le p_i \le i$) — the index of the vertex that is connected to vertex $i + 1$.
It is guaranteed that the sum of $n$ over all test cases does not exceed $5 \cdot 10^{5}$.
OutputFor each test case, output $n - 1$ integers. The $i$-th integer is the answer to the $i$-th query — the least number of operations required to make the current tree have two centroids.
We can show that an answer always exists.
ExampleInput5 2 1 3 1 1 4 1 2 3 7 1 2 3 2 5 2 10 1 2 2 4 5 5 7 8 9Output
0 0 1 0 1 0 0 1 0 1 2 3 0 1 2 1 0 1 0 1 2Note
The illustrations below are of the fourth example test case.
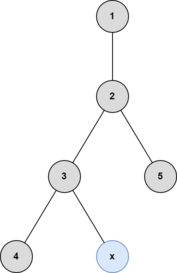
After the third query:
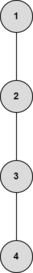
After the fourth query:
After the fifth query:
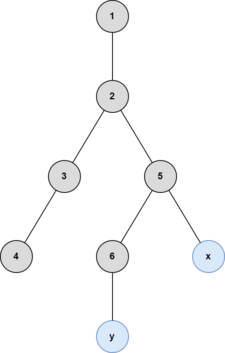
After the sixth query:
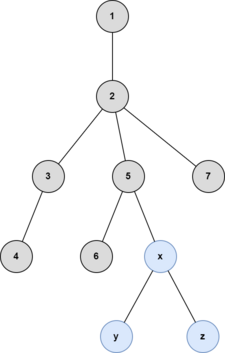
Input
题意翻译
地灵殿门口有一个小挂件,小挂件可视作一棵树,初始只有 $1$ 个编号为 $1$ 的节点。 接下来恋恋会做 $n-1$ 次操作,第 $i$ 次操作添加一个编号为 $i+1$ 的节点,并在节点 $i+1$ 与 $p_i$ 之间连边。 现在她想知道,在每一次操作之后,至少还需要进行多少次“新建一个点并与原树相连”的操作,才能使这棵树具有两个重心。 由于恋恋忙着给挂件做装饰,所以你要帮她解决这个问题。 本题有 $t$ 组数据。 ### 数据范围 - $1 \le t \le 10^4$ - $1 \le n \le 5 \cdot 10^5$ - $1 \le \sum n \le 5 \cdot 10^5$ - $1 \le p_i \le i$ - 给定输入均为正整数 ### 提示 树的重心的定义可参考[OI-wiki](https://oi-wiki.org/graph/tree-centroid/)。Output
给定一个初始仅包含顶点1的树(无向连通无环图)。会对这棵树进行多次查询。在第i次查询中,顶点i+1会出现并连接到顶点p_i(1≤p_i≤i)。每次查询后,请找出使当前树具有两个质心所需的最少操作数。在一次操作中,你可以向树中添加一个顶点和一个边,使得它仍然是一棵树。
一个顶点被称为质心,如果它的移除将树分割成顶点数不超过⌊n/2⌋的子树,其中n是树中顶点的数量。例如,在下面的树中,顶点3是质心,因为移除质心后最大的子树有2个顶点。
输入数据格式:
每个测试包含多个测试用例。第一行包含测试用例数t(1≤t≤10^4)。接下来是每个测试用例的描述。
每个测试用例的第一行包含一个整数n(2≤n≤5×10^5)——最终树的节点数。
每个测试用例的第二行包含n-1个整数p_1, p_2, …, p_{n-1}(1≤p_i≤i)——连接到顶点i+1的顶点的索引。
输出数据格式:
对于每个测试用例,输出n-1个整数。第i个整数是对第i个查询的答案——使当前树具有两个质心所需的最少操作数。题目大意: 给定一个初始仅包含顶点1的树(无向连通无环图)。会对这棵树进行多次查询。在第i次查询中,顶点i+1会出现并连接到顶点p_i(1≤p_i≤i)。每次查询后,请找出使当前树具有两个质心所需的最少操作数。在一次操作中,你可以向树中添加一个顶点和一个边,使得它仍然是一棵树。 一个顶点被称为质心,如果它的移除将树分割成顶点数不超过⌊n/2⌋的子树,其中n是树中顶点的数量。例如,在下面的树中,顶点3是质心,因为移除质心后最大的子树有2个顶点。 输入数据格式: 每个测试包含多个测试用例。第一行包含测试用例数t(1≤t≤10^4)。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数n(2≤n≤5×10^5)——最终树的节点数。 每个测试用例的第二行包含n-1个整数p_1, p_2, …, p_{n-1}(1≤p_i≤i)——连接到顶点i+1的顶点的索引。 输出数据格式: 对于每个测试用例,输出n-1个整数。第i个整数是对第i个查询的答案——使当前树具有两个质心所需的最少操作数。