310398: CF1827E. Bus Routes

E. Bus Routestime limit per test2.5 secondsmemory limit per test1024 megabytesinputstandard inputoutputstandard output

There is a country consisting of $n$ cities and $n - 1$ bidirectional roads connecting them such that we can travel between any two cities using these roads. In other words, these cities and roads form a tree.

There are $m$ bus routes connecting the cities together. A bus route between city $x$ and city $y$ allows you to travel between any two cities in the simple path between $x$ and $y$ with this route.

Determine if for every pair of cities $u$ and $v$, you can travel from $u$ to $v$ using at most two bus routes.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \le t \le 10^4$). The description of the test cases follows.

The first line of each test case contains two integers $n$ and $m$ ($2 \le n \le 5 \cdot 10^5, 0 \le m \le 5 \cdot 10^5$) — the number of cities and the number of bus routes.

Then $n - 1$ lines follow. Each line contains two integers $u$ and $v$ denoting a road connecting city $u$ and city $v$ ($1 \le u, v \le n, u \neq v$). It is guaranteed that these cities and roads form a tree.

Then $m$ lines follow. Each line contains two integers $x$ and $y$ denoting a bus route between city $x$ and city $y$ ($1 \le x, y \le n$).

It is guaranteed that the sum of $n$ over all test cases does not exceed $5 \cdot 10^5$ and the sum of $m$ over all test cases does not exceed $5 \cdot 10^5$.

Output

For each test case, output "YES" if you can travel between any pair of cities using at most two bus routes.

Otherwise, output "NO". In the next line, output two cities $x$ and $y$ ($1 \le x, y \le n$) such that it is impossible to reach city $y$ from city $x$ using at most two bus routes.

You can output the answer in any case (upper or lower). For example, the strings "yEs", "yes", "Yes", and "YES" will be recognized as positive responses.

ExampleInput

4
5 2
1 2
2 3
3 4
2 5
1 4
5 2
5 1
1 2
2 3
3 4
2 5
1 5
2 0
1 2
6 3
1 2
2 3
3 4
4 5
5 6
1 3
2 5
4 6

Output

YES
NO
1 3
NO
1 2
NO
1 6

Note

Here are the graphs of test case $1$, $2$, and $4$:

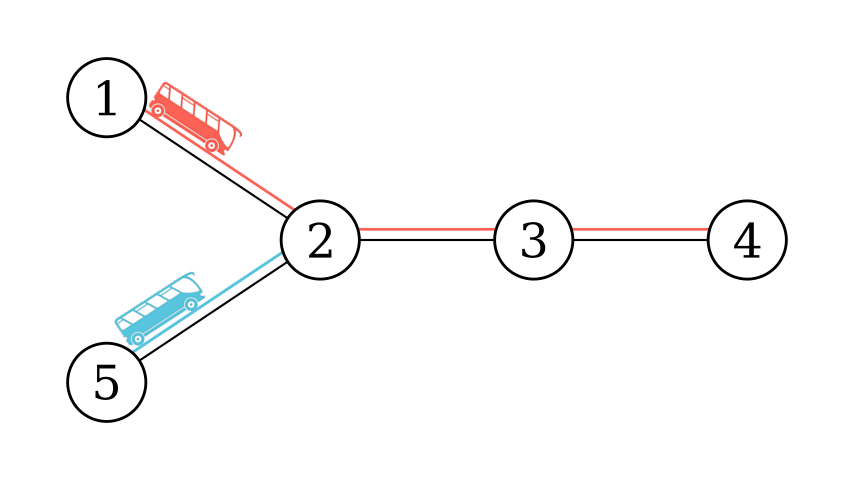Sample 1 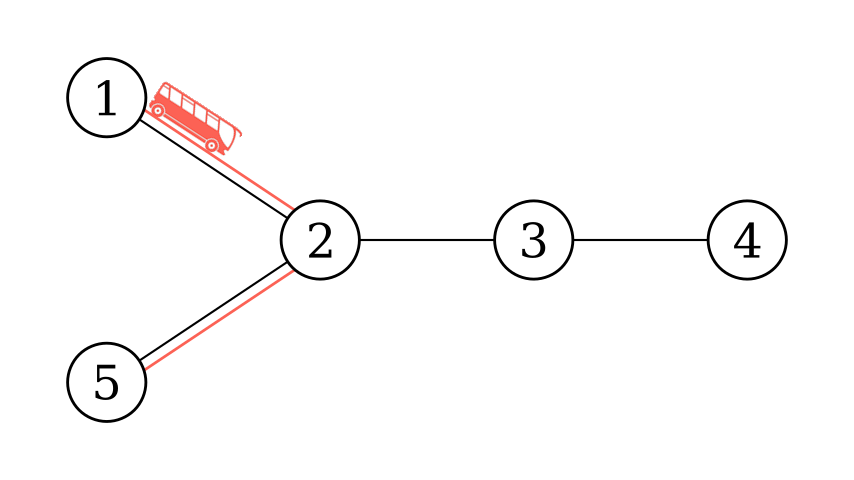Sample 2 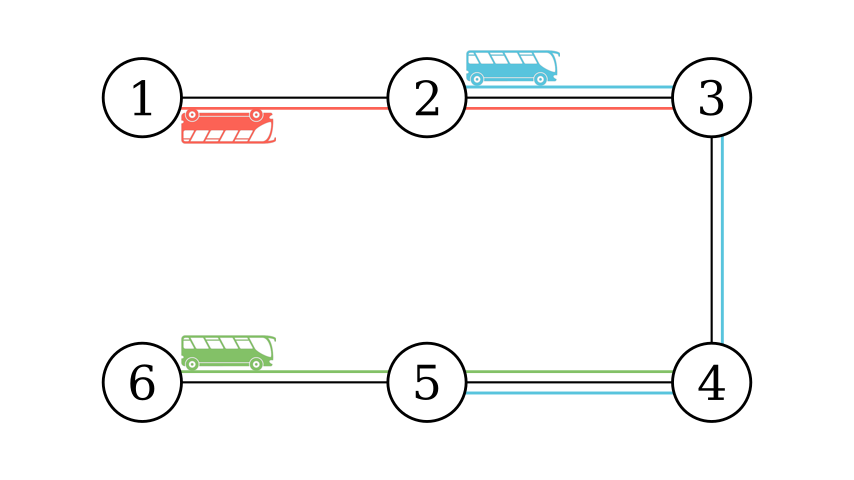Sample 4

题目大意：
E. 公交路线
有一个由 n 个城市和 n-1 条双向道路组成的国度，通过这些道路可以任意两个城市间旅行，即这些城市和道路形成了一棵树。有 m 条公交路线连接这些城市，一条连接城市 x 和城市 y 的公交路线允许你使用这条路线在 x 和 y 之间的简单路径上的任意两个城市间旅行。确定是否对于每对城市 u 和 v，你可以使用最多两条公交路线从 u 旅行到 v。

输入数据格式：
每个测试包含多个测试案例。第一行包含测试案例的数量 t (1 ≤ t ≤ 10^4)。接下来是测试案例的描述。
每个测试案例的第一行包含两个整数 n 和 m (2 ≤ n ≤ 5 × 10^5, 0 ≤ m ≤ 5 × 10^5) —— 城市数量和公交路线数量。
然后是 n-1 行，每行包含两个整数 u 和 v，表示连接城市 u 和城市 v 的道路 (1 ≤ u, v ≤ n, u ≠ v)。保证这些城市和道路形成一棵树。
然后是 m 行，每行包含两个整数 x 和 y，表示连接城市 x 和城市 y 的公交路线 (1 ≤ x, y ≤ n)。
保证所有测试案例的 n 之和不超过 5 × 10^5，m 之和不超过 5 × 10^5。

输出数据格式：
对于每个测试案例，如果可以使用最多两条公交路线在任意两对城市间旅行，输出 "YES"。
否则，输出 "NO"。在下一行，输出两个城市 x 和 y (1 ≤ x, y ≤ n)，使得无法使用最多两条公交路线从城市 x 到达城市 y。
答案可以是任何大小写形式，例如 "yEs"、"yes"、"Yes" 和 "YES" 都会被认为是肯定的回答。题目大意： E. 公交路线 有一个由 n 个城市和 n-1 条双向道路组成的国度，通过这些道路可以任意两个城市间旅行，即这些城市和道路形成了一棵树。有 m 条公交路线连接这些城市，一条连接城市 x 和城市 y 的公交路线允许你使用这条路线在 x 和 y 之间的简单路径上的任意两个城市间旅行。确定是否对于每对城市 u 和 v，你可以使用最多两条公交路线从 u 旅行到 v。 输入数据格式： 每个测试包含多个测试案例。第一行包含测试案例的数量 t (1 ≤ t ≤ 10^4)。接下来是测试案例的描述。 每个测试案例的第一行包含两个整数 n 和 m (2 ≤ n ≤ 5 × 10^5, 0 ≤ m ≤ 5 × 10^5) —— 城市数量和公交路线数量。 然后是 n-1 行，每行包含两个整数 u 和 v，表示连接城市 u 和城市 v 的道路 (1 ≤ u, v ≤ n, u ≠ v)。保证这些城市和道路形成一棵树。 然后是 m 行，每行包含两个整数 x 和 y，表示连接城市 x 和城市 y 的公交路线 (1 ≤ x, y ≤ n)。 保证所有测试案例的 n 之和不超过 5 × 10^5，m 之和不超过 5 × 10^5。 输出数据格式： 对于每个测试案例，如果可以使用最多两条公交路线在任意两对城市间旅行，输出 "YES"。 否则，输出 "NO"。在下一行，输出两个城市 x 和 y (1 ≤ x, y ≤ n)，使得无法使用最多两条公交路线从城市 x 到达城市 y。 答案可以是任何大小写形式，例如 "yEs"、"yes"、"Yes" 和 "YES" 都会被认为是肯定的回答。