Li Hua and Path

题意翻译

刚开始给定一个 $n$ 个点的树。 对于一棵树上，如果有两个点 $u<v$ 满足下面两个条件恰有一个成立，那么 $(u,v)$ 就是个好对子。 条件： 1. $u$ 是 $u\to v$ 路径上**编号**最小的点 2. $v$ 是 $u\to v$ 路径上**编号**最大的点 有 $m$ 个修改，给出一个数 $x<n+i$，第 $i$ 次修改加入一个编号为 $n+i$ 的点，以 $x$ 点为父亲。 输出共 $m+1$ 行，输出刚开始和每次修改后好对子的个数。

题目描述

Li Hua has a tree of $ n $ vertices and $ n-1 $ edges. The vertices are numbered from $ 1 $ to $ n $ . A pair of vertices $ (u,v) $ ( $ u < v $ ) is considered cute if exactly one of the following two statements is true: - $ u $ is the vertex with the minimum index among all vertices on the path $ (u,v) $ . - $ v $ is the vertex with the maximum index among all vertices on the path $ (u,v) $ . There will be $ m $ operations. In each operation, he decides an integer $ k_j $ , then inserts a vertex numbered $ n+j $ to the tree, connecting with the vertex numbered $ k_j $ . He wants to calculate the number of cute pairs before operations and after each operation. Suppose you were Li Hua, please solve this problem.

输入输出格式

输入格式

The first line contains the single integer $ n $ ( $ 2\le n\le 2\cdot 10^5 $ ) — the number of vertices in the tree. Next $ n-1 $ lines contain the edges of the tree. The $ i $ -th line contains two integers $ u_i $ and $ v_i $ ( $ 1\le u_i,v_i\le n $ ; $ u_i\ne v_i $ ) — the corresponding edge. The given edges form a tree. The next line contains the single integer $ m $ ( $ 1\le m\le 2\cdot 10^5 $ ) — the number of operations. Next $ m $ lines contain operations — one operation per line. The $ j $ -th operation contains one integer $ k_j $ ( $ 1\le k_j < n+j $ ) — a vertex.

输出格式

Print $ m+1 $ integers — the number of cute pairs before operations and after each operation.

输入输出样例

输入样例 #1

7
2 1
1 3
1 4
4 6
4 7
6 5
2
5
6

输出样例 #1

11
15
19

说明

The initial tree is shown in the following picture: 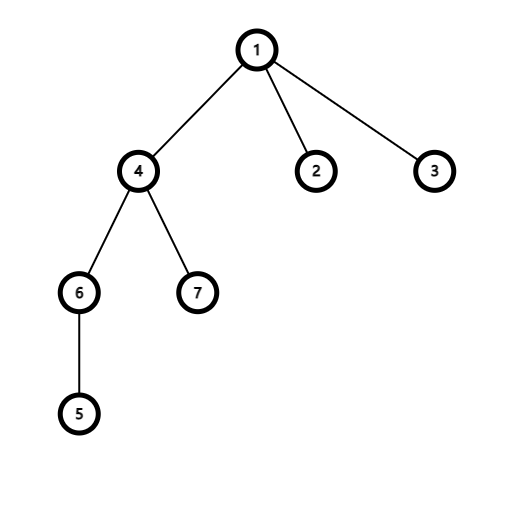There are $ 11 $ cute pairs — $ (1,5),(2,3),(2,4),(2,6),(2,7),(3,4),(3,6),(3,7),(4,5),(5,7),(6,7) $ . Similarly, we can count the cute pairs after each operation and the result is $ 15 $ and $ 19 $ .

**题目大意：**

给定一棵有 $ n $ 个节点和 $ n-1 $ 条边的树，节点的编号从 $ 1 $ 到 $ n $。两个节点 $ u $ 和 $ v $（$ u < v $）组成的对子 $(u,v)$ 如果满足以下两个条件中的恰好一个，则被认为是一个“好对子”：

1. $ u $ 是从 $ u $ 到 $ v $ 路径上编号最小的节点。
2. $ v $ 是从 $ u $ 到 $ v $ 路径上编号最大的节点。

接下来会有 $ m $ 次操作，每次操作确定一个整数 $ k_j $，然后向树中插入一个编号为 $ n+j $ 的节点，并与之连接到编号为 $ k_j $ 的节点。

需要计算在操作之前和每次操作之后“好对子”的数量。

**输入输出格式：**

**输入格式：**

- 第一行包含一个整数 $ n $（$ 2 \le n \le 2 \cdot 10^5 $）——树中节点的数量。
- 接下来的 $ n-1 $ 行包含树的边。第 $ i $ 行包含两个整数 $ u_i $ 和 $ v_i $（$ 1 \le u_i, v_i \le n $；$ u_i \ne v_i $）——对应的边。给定的边构成一棵树。
- 下一行包含一个整数 $ m $（$ 1 \le m \le 2 \cdot 10^5 $）——操作的数量。
- 接下来的 $ m $ 行包含每次操作——每行一个操作。第 $ j $ 次操作包含一个整数 $ k_j $（$ 1 \le k_j < n+j $）——一个节点的编号。

**输出格式：**

- 输出 $ m+1 $ 个整数——操作之前和每次操作之后的“好对子”数量。

**输入输出样例：**

**输入样例 #1:**
```
7
2 1
1 3
1 4
4 6
4 7
6 5
2
5
6
```

**输出样例 #1:**
```
11
15
19
```

**说明：**

初始的树如上图所示。有 $ 11 $ 个“好对子”——$(1,5),(2,3),(2,4),(2,6),(2,7),(3,4),(3,6),(3,7),(4,5),(5,7),(6,7)$。

同样地，我们可以计算每次操作后的“好对子”数量，结果分别是 $ 15 $ 和 $ 19 $。**题目大意：** 给定一棵有 $ n $ 个节点和 $ n-1 $ 条边的树，节点的编号从 $ 1 $ 到 $ n $。两个节点 $ u $ 和 $ v $（$ u < v $）组成的对子 $(u,v)$ 如果满足以下两个条件中的恰好一个，则被认为是一个“好对子”： 1. $ u $ 是从 $ u $ 到 $ v $ 路径上编号最小的节点。 2. $ v $ 是从 $ u $ 到 $ v $ 路径上编号最大的节点。 接下来会有 $ m $ 次操作，每次操作确定一个整数 $ k_j $，然后向树中插入一个编号为 $ n+j $ 的节点，并与之连接到编号为 $ k_j $ 的节点。 需要计算在操作之前和每次操作之后“好对子”的数量。 **输入输出格式：** **输入格式：** - 第一行包含一个整数 $ n $（$ 2 \le n \le 2 \cdot 10^5 $）——树中节点的数量。 - 接下来的 $ n-1 $ 行包含树的边。第 $ i $ 行包含两个整数 $ u_i $ 和 $ v_i $（$ 1 \le u_i, v_i \le n $；$ u_i \ne v_i $）——对应的边。给定的边构成一棵树。 - 下一行包含一个整数 $ m $（$ 1 \le m \le 2 \cdot 10^5 $）——操作的数量。 - 接下来的 $ m $ 行包含每次操作——每行一个操作。第 $ j $ 次操作包含一个整数 $ k_j $（$ 1 \le k_j < n+j $）——一个节点的编号。 **输出格式：** - 输出 $ m+1 $ 个整数——操作之前和每次操作之后的“好对子”数量。 **输入输出样例：** **输入样例 #1:** ``` 7 2 1 1 3 1 4 4 6 4 7 6 5 2 5 6 ``` **输出样例 #1:** ``` 11 15 19 ``` **说明：** 初始的树如上图所示。有 $ 11 $ 个“好对子”——$(1,5),(2,3),(2,4),(2,6),(2,7),(3,4),(3,6),(3,7),(4,5),(5,7),(6,7)$。 同样地，我们可以计算每次操作后的“好对子”数量，结果分别是 $ 15 $ 和 $ 19 $。