Li Hua and Tree

题意翻译

李华有一棵 $n$ 个节点的有根树，根节点为 $1$，第 $i$ 个节点有点权 $a_i$。定义一个非叶子节点的重儿子 $son$ 为子树内点数最大的，若有多个则取编号最小的。 维护 $m$ 次操作： - 操作一：求以 $x$ 为根的子树内的点权和。 - 操作二：切断 $(x,{fa}_x)$ 之间的边，在 $({son}_x,{fa}_x)$ 之间连一条边。如果 $x$ 为叶子，忽略这次操作。 假如你是李华，请解决这一问题。 （[全场中文题面](https://www.cnblogs.com/ruierqwq/p/CF1797-CHN-statement.html)）

题目描述

Li Hua has a tree of $ n $ vertices and $ n-1 $ edges. The root of the tree is vertex $ 1 $ . Each vertex $ i $ has importance $ a_i $ . Denote the size of a subtree as the number of vertices in it, and the importance as the sum of the importance of vertices in it. Denote the heavy son of a non-leaf vertex as the son with the largest subtree size. If multiple of them exist, the heavy son is the one with the minimum index. Li Hua wants to perform $ m $ operations: - "1 $ x $ " ( $ 1\leq x \leq n $ ) — calculate the importance of the subtree whose root is $ x $ . - "2 $ x $ " ( $ 2\leq x \leq n $ ) — rotate the heavy son of $ x $ up. Formally, denote $ son_x $ as the heavy son of $ x $ , $ fa_x $ as the father of $ x $ . He wants to remove the edge between $ x $ and $ fa_x $ and connect an edge between $ son_x $ and $ fa_x $ . It is guaranteed that $ x $ is not root, but not guaranteed that $ x $ is not a leaf. If $ x $ is a leaf, please ignore the operation. Suppose you were Li Hua, please solve this problem.

输入输出格式

输入格式

The first line contains 2 integers $ n,m $ ( $ 2\le n\le 10^{5},1\le m\le 10^{5} $ ) — the number of vertices in the tree and the number of operations. The second line contains $ n $ integers $ a_{1},a_{2},\ldots ,a_{n} $ ( $ -10^{9}\le a_{i}\le 10^{9} $ ) — the importance of each vertex. Next $ n-1 $ lines contain the edges of the tree. The $ i $ -th line contains two integers $ u_i $ and $ v_i $ ( $ 1\le u_i,v_i\le n $ , $ u_i\ne v_i $ ) — the corresponding edge. The given edges form a tree. Next $ m $ lines contain operations — one operation per line. The $ j $ -th operation contains two integers $ t_{j},x_{j} $ ( $ t_{j}\in \{1,2\} $ , $ 1 \leq x_{j} \leq n $ , $ x_{j}\neq 1 $ if $ t_j = 2 $ ) — the $ j $ -th operation.

输出格式

For each query "1 $ x $ ", output the answer in an independent line.

输入输出样例

输入样例 #1

7 4
1 1 1 1 1 1 1
1 2
1 3
2 4
2 5
3 6
6 7
1 6
2 3
1 6
1 2

输出样例 #1

2
3
3

输入样例 #2

10 14
-160016413 -90133231 -671446275 -314847579 -910548234 121155052 -359359950 83112406 -704889624 145489303
1 6
1 10
10 8
1 4
3 4
2 7
2 5
3 2
9 8
1 4
2 2
2 4
1 4
1 10
2 10
1 9
1 6
2 8
2 10
1 5
1 8
1 1
2 5

输出样例 #2

-2346335269
-314847579
-476287915
-704889624
121155052
-1360041415
228601709
-2861484545

说明

In the first example: The initial tree is shown in the following picture: The importance of the subtree of $ 6 $ is $ a_6+a_7=2 $ . After rotating the heavy son of $ 3 $ (which is $ 6 $ ) up, the tree is shown in the following picture: 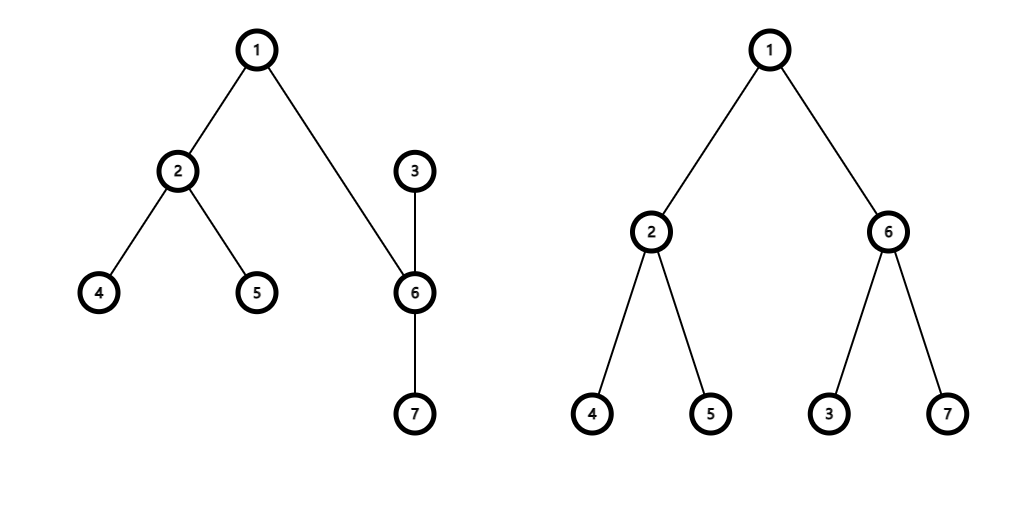The importance of the subtree of $ 6 $ is $ a_6+a_3+a_7=3 $ . The importance of the subtree of $ 2 $ is $ a_2+a_4+a_5=3 $ .

题目大意：
李华有一棵n个节点的有根树，根节点为1，每个节点i有点权a_i。定义一个非叶子节点的重儿子son为子树内点数最大的，若有多个则取编号最小的。

维护m次操作：

1. 求以x为根的子树内的点权和。
2. 切断(x,fa_x)之间的边，在(son_x,fa_x)之间连一条边。如果x为叶子，忽略这次操作。

输入输出数据格式：

输入格式：
- 第一行包含2个整数n,m（2≤n≤10^5,1≤m≤10^5）——树的节点数和操作数。
- 第二行包含n个整数a_1,a_2,…,a_n（-10^9≤a_i≤10^9）——每个节点的重要性。
- 接下来n-1行包含树的边。第i行包含两个整数u_i和v_i（1≤u_i,v_i≤n,u_i≠v_i）——对应的边。给定的边构成一棵树。
- 接下来m行包含操作——每行一个操作。第j个操作包含两个整数t_j,x_j（t_j∈{1,2},1≤x_j≤n,x_j≠1如果t_j=2）——第j个操作。

输出格式：
- 对于每个查询"1 x"，在独立的一行中输出答案。题目大意： 李华有一棵n个节点的有根树，根节点为1，每个节点i有点权a_i。定义一个非叶子节点的重儿子son为子树内点数最大的，若有多个则取编号最小的。 维护m次操作： 1. 求以x为根的子树内的点权和。 2. 切断(x,fa_x)之间的边，在(son_x,fa_x)之间连一条边。如果x为叶子，忽略这次操作。 输入输出数据格式： 输入格式： - 第一行包含2个整数n,m（2≤n≤10^5,1≤m≤10^5）——树的节点数和操作数。 - 第二行包含n个整数a_1,a_2,…,a_n（-10^9≤a_i≤10^9）——每个节点的重要性。 - 接下来n-1行包含树的边。第i行包含两个整数u_i和v_i（1≤u_i,v_i≤n,u_i≠v_i）——对应的边。给定的边构成一棵树。 - 接下来m行包含操作——每行一个操作。第j个操作包含两个整数t_j,x_j（t_j∈{1,2},1≤x_j≤n,x_j≠1如果t_j=2）——第j个操作。 输出格式： - 对于每个查询"1 x"，在独立的一行中输出答案。