Li Hua and Chess

题意翻译

**本题是一道交互题。** 李明和李华在玩游戏。李华有一个大小为 $n\times m$ 的国际象棋棋盘。李明在棋盘上放置了一个国王，李华需要猜出他的位置。 李华可以问李明**不超过 $3$ 个**问题。对于每个问题，他可以选择一个格子并询问国王移动到那里的最小步数。每个问题相互独立，也就是说国王不会真的移动。 国王可以从 $(x,y)$ 移动到 $(x',y')$，当且仅当 $\max\{|x-x'|,|y-y'|\}=1$（如下图所示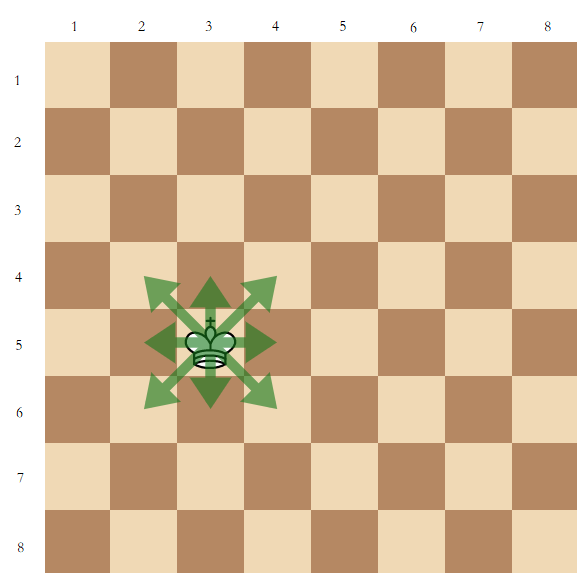）。  国王的位置**在交互前**被确定。 假如你是李华，请解决这一问题。 （[全场中文题面](https://www.cnblogs.com/ruierqwq/p/CF1797-CHN-statement.html)）

题目描述

This is an interactive problem. Li Ming and Li Hua are playing a game. Li Hua has a chessboard of size $ n\times m $ . Denote $ (r, c) $ ( $ 1\le r\le n, 1\le c\le m $ ) as the cell on the $ r $ -th row from the top and on the $ c $ -th column from the left. Li Ming put a king on the chessboard and Li Hua needs to guess its position. Li Hua can ask Li Ming no more than $ 3 $ questions. In each question, he can choose a cell and ask the minimum steps needed to move the king to the chosen cell. Each question is independent, which means the king doesn't actually move. A king can move from $ (x,y) $ to $ (x',y') $ if and only if $ \max\{|x-x'|,|y-y'|\}=1 $ (shown in the following picture). 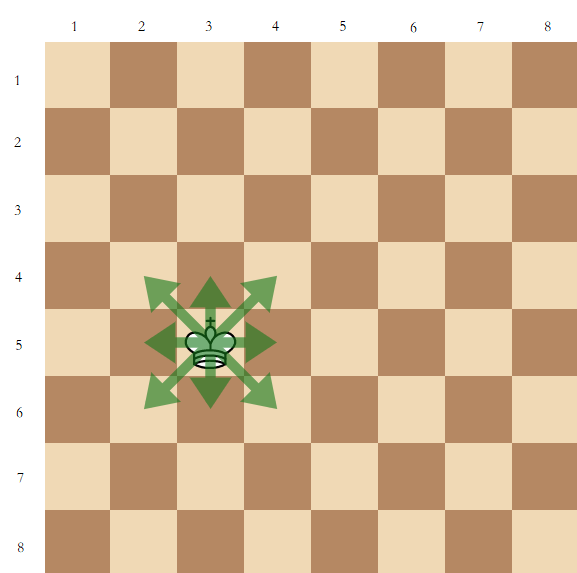The position of the king is chosen before the interaction. Suppose you were Li Hua, please solve this problem.

输入输出格式

输入格式

输出格式

The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^3 $ ). The first line of each test case contains two integers $ n,m $ ( $ 1\le n,m\le 10^9 $ ) — the size of the chessboard, and then the interaction begins. To ask a question, print "? $ r $ $ c $ " (without quotes, $ 1 \leq r \leq n, 1 \leq c \leq m $ ). Then you should input the response from standard input — the minimum steps the king needs to move to the chosen cell. If your program has asked an invalid question or has run out of questions, the interactor will terminate immediately and your program will get a verdict Wrong answer. To give the final answer, print "! $ r $ $ c $ " (without the quotes, $ (r,c) $ is the king's initial coordinate). Note that giving this answer is not counted towards the limit of $ 3 $ questions. After asking a question do not forget to output the end of line and flush the output. Otherwise, you will get Idleness limit exceeded. To do this, use: - fflush(stdout) or cout.flush() in C++; - System.out.flush() in Java; - flush(output) in Pascal; - stdout.flush() in Python; - see the documentation for other languages. Hacks To hack, use the following format. The first line should contain a single integer $ t $ ( $ 1 \le t \le 10^3 $ ). The first and only line of each test case should contain four integers $ n,m,r,c $ ( $ 1\le r\le n\le 10^9,1\le c\le m\le 10^9 $ ).

输入输出样例

输入样例 #1

2
3 4

1

2

5 3

3

1

2

输出样例 #1

? 2 3

? 2 4

! 2 2

? 2 2

? 5 2

? 5 3

! 5 1

说明

In test case 1, the king is at $ (2,2) $ . It takes $ 1 $ step to move to $ (2,3) $ and $ 2 $ steps to move to $ (2,4) $ . 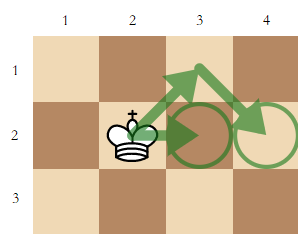Note that the questions may not seem sensible. They are just a sample of questions you may ask.

**题目大意：**
这是一道交互题。李明和李华在玩游戏。李华有一个大小为 $n \times m$ 的国际象棋棋盘。李明在棋盘上放置了一个国王，李华需要猜出他的位置。李华可以问李明**不超过 3 个**问题。对于每个问题，他可以选择一个格子并询问国王移动到那里的最小步数。每个问题相互独立，也就是说国王不会真的移动。国王可以从 $(x,y)$ 移动到 $(x',y')$，当且仅当 $\max\{|x-x'|,|y-y'|\}=1$。国王的位置**在交互前**被确定。

**输入输出数据格式：**
- **输入格式：**
- 第一行包含测试用例的数量 $t$（$1 \le t \le 10^3$）。
- 每个测试用例的第一行包含两个整数 $n, m$（$1 \le n, m \le 10^9$）—— 棋盘的大小，然后开始交互。
- 为了提问，输出 "? $r$ $c$" （不包含引号，$1 \leq r \leq n, 1 \leq c \leq m$）。然后你应该从标准输入中输入回应——国王移动到所选格子的最小步数。
- **输出格式：**
- 当你确定国王的位置时，输出 "! $r$ $c$" （不包含引号，$(r,c)$ 是国王的初始坐标）。注意，给出这个答案不计入3个问题的限制。
- 在提问后不要忘记输出换行符并刷新输出。否则，你将得到“空闲超时”。具体操作方式因编程语言而异。

**输入输出样例：**
- **输入样例 #1：**
```
2
3 4
1
2
5 3
3
1
2
```
- **输出样例 #1：**
```
? 2 3
? 2 4
! 2 2
? 2 2
? 5 2
? 5 3
! 5 1
```
- **说明：**
在样例1中，国王位于 $(2,2)$。移动到 $(2,3)$ 需要 1 步，移动到 $(2,4)$ 需要 2 步。注意，提出的问题可能看起来没有意义。它们只是你可能提出的问题的一个示例。**题目大意：** 这是一道交互题。李明和李华在玩游戏。李华有一个大小为 $n \times m$ 的国际象棋棋盘。李明在棋盘上放置了一个国王，李华需要猜出他的位置。李华可以问李明**不超过 3 个**问题。对于每个问题，他可以选择一个格子并询问国王移动到那里的最小步数。每个问题相互独立，也就是说国王不会真的移动。国王可以从 $(x,y)$ 移动到 $(x',y')$，当且仅当 $\max\{|x-x'|,|y-y'|\}=1$。国王的位置**在交互前**被确定。 **输入输出数据格式：** - **输入格式：** - 第一行包含测试用例的数量 $t$（$1 \le t \le 10^3$）。 - 每个测试用例的第一行包含两个整数 $n, m$（$1 \le n, m \le 10^9$）—— 棋盘的大小，然后开始交互。 - 为了提问，输出 "? $r$ $c$" （不包含引号，$1 \leq r \leq n, 1 \leq c \leq m$）。然后你应该从标准输入中输入回应——国王移动到所选格子的最小步数。 - **输出格式：** - 当你确定国王的位置时，输出 "! $r$ $c$" （不包含引号，$(r,c)$ 是国王的初始坐标）。注意，给出这个答案不计入3个问题的限制。 - 在提问后不要忘记输出换行符并刷新输出。否则，你将得到“空闲超时”。具体操作方式因编程语言而异。 **输入输出样例：** - **输入样例 #1：** ``` 2 3 4 1 2 5 3 3 1 2 ``` - **输出样例 #1：** ``` ? 2 3 ? 2 4 ! 2 2 ? 2 2 ? 5 2 ? 5 3 ! 5 1 ``` - **说明：** 在样例1中，国王位于 $(2,2)$。移动到 $(2,3)$ 需要 1 步，移动到 $(2,4)$ 需要 2 步。注意，提出的问题可能看起来没有意义。它们只是你可能提出的问题的一个示例。