Kirill and Company

题意翻译

### 题意 给一个无向连通图，有 $f$ 个朋友在节点1，每个人的家在 $h_i$ ，其中有 $k(k \leq 6)$ 个朋友没有车，有车的朋友可以开车载任意数量的**顺路**的朋友回家。问最后无法被开车送回的朋友的最小数量。 **顺路**：他的家在有车朋友回家的最短路上的朋友

题目描述

Kirill lives on a connected undirected graph of $ n $ vertices and $ m $ edges at vertex $ 1 $ . One fine evening he gathered $ f $ friends, the $ i $ -th friend lives at the vertex $ h_i $ . So all friends are now in the vertex $ 1 $ , the $ i $ -th friend must get to his home to the vertex $ h_i $ . The evening is about to end and it is time to leave. It turned out that $ k $ ( $ k \le 6 $ ) of his friends have no cars, and they would have to walk if no one gives them a ride. One friend with a car can give a ride to any number of friends without cars, but only if he can give them a ride by driving along one of the shortest paths to his house. For example, in the graph below, a friend from vertex $ h_i=5 $ can give a ride to friends from the following sets of vertices: $ [2, 3] $ , $ [2, 4] $ , $ [2] $ , $ [3] $ , $ [4] $ , but can't give a ride to friend from vertex $ 6 $ or a set $ [3, 4] $ . 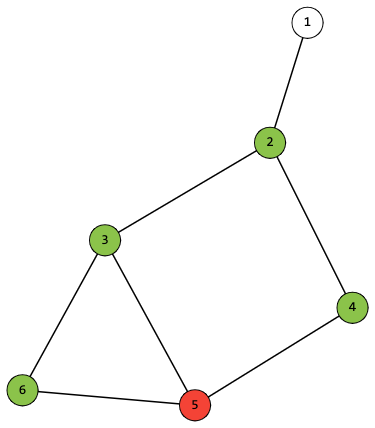The vertices where friends without cars live are highlighted in green, and with cars — in red.Kirill wants as few friends as possible to have to walk. Help him find the minimum possible number.

输入输出格式

输入格式

The first line of input data contains an integer $ t $ ( $ 1 \le t \le 10^3 $ ) — the number of test cases in the test. The first line of the test case contains two integers $ n $ and $ m $ ( $ 2 \le n \le 10^4 $ , $ n-1 \le m \le min (10^4, $ $ \frac{n \cdot (n - 1)}{2} $ $ ) $ ) — the number of vertices and edges, respectively. The next $ m $ lines of the test case contain a description of the edges, two integers each $ u $ and $ v $ ( $ 1 \le u, v \le n $ , $ u \ne v $ ) — indexes of vertices connected by an edge. It is guaranteed that there is at most one edge between any pair of vertices (i.e. no multiple edges in the graph). Then follows line containing the number $ f $ ( $ 1 \le f \le 10^4 $ ) — the number of Kirill's friends. The next line of the test case contains $ f $ integers: $ h_1, h_2, \dots, h_f $ ( $ 2 \le h_i \le n $ ) — the vertices in which they live. Some vertices may be repeated. The next line of the set contains the number $ k $ ( $ 1 \le k \le min(6, f) $ ) — the number of friends without cars. The last line of each test case contains $ k $ integers: $ p_1, p_2, \dots, p_k $ ( $ 1 \le p_i \le f $ , $ p_i < p_{i+1} $ ) — indexes of friends without cars. It is guaranteed that the sum of $ n $ over all cases does not exceed $ 10^4 $ , as well as the sums of $ m $ and $ f $ .

输出格式

Output $ t $ lines, each of which contains the answer to the corresponding test case. As an answer, output a single integer — the minimum possible number of friends who will have to walk.

输入输出样例

输入样例 #1

3
6 7
1 2
2 3
2 4
3 5
4 5
3 6
6 5
5
2 3 4 5 6
4
1 2 3 5
6 7
1 2
2 3
2 4
3 5
4 5
3 6
6 5
6
2 3 4 5 6 5
4
1 2 3 5
4 4
1 2
1 3
2 3
3 4
3
3 4 2
2
1 3

输出样例 #1

2
1
1

输入样例 #2

3
2 1
1 2
3
2 2 2
3
1 2 3
3 3
1 2
1 3
2 3
4
2 2 2 3
3
1 2 4
4 4
3 1
3 2
1 4
2 4
5
3 2 2 4 2
3
1 3 4

输出样例 #2

3
1
0

说明

The first test case of the first example is explained in the statement. In the second test case of the first example, two friends with cars live at vertex $ 5 $ , one can give a ride to friends from vertices $ 2 $ and $ 3 $ , and the second from vertex $ 4 $ , only a friend from vertex $ 6 $ will have to walk.

题目大意：
Kirill 住在由 n 个顶点和 m 条边组成的无向连通图中，位于顶点 1。一天晚上，他聚集了 f 个朋友，第 i 个朋友住在顶点 h_i。现在所有朋友都在顶点 1，第 i 个朋友必须回到他的家顶点 h_i。

晚上即将结束，是时候离开了。结果发现，有 k（k ≤ 6）个朋友没有车，如果没有人载他们，他们只能步行。一个有车的朋友可以载任意数量的没有车的朋友，但只有在沿着到他家的一条最短路径开车时才可以。

例如，在下面的图中，来自顶点 h_i=5 的朋友可以载来自以下顶点集合的朋友：[2, 3], [2, 4], [2], [3], [4]，但不能载来自顶点 6 或集合 [3, 4] 的朋友。

图中没有车的朋友住的顶点用绿色标出，有车的朋友用红色标出。Kirill 希望尽可能少的朋友步行。帮助他找出最小的可能数量。

输入输出格式：
输入格式：
第一行输入数据包含一个整数 t（1 ≤ t ≤ 10^3）——测试用例的数量。

每个测试用例的第一行包含两个整数 n 和 m（2 ≤ n ≤ 10^4，n-1 ≤ m ≤ min(10^4, n(n - 1)/2)）——顶点的数量和边的数量。

接下来的 m 行包含边的描述，每行两个整数 u 和 v（1 ≤ u, v ≤ n，u ≠ v）——由边连接的顶点的索引。保证任意两个顶点之间最多有一条边（即图中没有多条边）。

然后是一行包含数字 f（1 ≤ f ≤ 10^4）——Kirill 的朋友的数量。

接下来的一行包含 f 个整数：h_1, h_2, ..., h_f（2 ≤ h_i ≤ n）——他们居住的顶点。可能有重复的顶点。

接下来的一行包含数字 k（1 ≤ k ≤ min(6, f)）——没有车的朋友的数量。

每个测试用例的最后一行包含 k 个整数：p_1, p_2, ..., p_k（1 ≤ p_i ≤ f，p_i < p_{i+1}）——没有车的朋友的索引。

保证所有案例的 n 之和不超过 10^4，m 和 f 的总和也是如此。

输出格式：
输出 t 行，每行包含对应测试用例的答案。作为答案，输出一个整数——将不得不步行的朋友的最小可能数量。

输入输出样例：
输入样例 #1：
3
6 7
1 2
2 3
2 4
3 5
4 5
3 6
6 5
5
2 3 4 5 6
4
1 2 3 5
6 7
1 2
2 3
2 4
3 5
4 5
3 6
6 5
6
2 3 4 5 6 5
4
1 2 3 5
4 4
1 2
1 3
2 3
3 4
3
3 4 2
2
1 3
输出样例 #1：
2
1
1

输入样例 #2：
3
2 1
1 2
3
2 2 2
3
1 2 3
3 3
1 2
1 3
2 3
4
2 2 2 3
3
1 2 4
4 4
3 1
3 2
1 4
2 4
5
3 2 2 4 2
3
1 3 4
输出样例 #2：
3
1
0题目大意： Kirill 住在由 n 个顶点和 m 条边组成的无向连通图中，位于顶点 1。一天晚上，他聚集了 f 个朋友，第 i 个朋友住在顶点 h_i。现在所有朋友都在顶点 1，第 i 个朋友必须回到他的家顶点 h_i。 晚上即将结束，是时候离开了。结果发现，有 k（k ≤ 6）个朋友没有车，如果没有人载他们，他们只能步行。一个有车的朋友可以载任意数量的没有车的朋友，但只有在沿着到他家的一条最短路径开车时才可以。 例如，在下面的图中，来自顶点 h_i=5 的朋友可以载来自以下顶点集合的朋友：[2, 3], [2, 4], [2], [3], [4]，但不能载来自顶点 6 或集合 [3, 4] 的朋友。 图中没有车的朋友住的顶点用绿色标出，有车的朋友用红色标出。Kirill 希望尽可能少的朋友步行。帮助他找出最小的可能数量。 输入输出格式： 输入格式： 第一行输入数据包含一个整数 t（1 ≤ t ≤ 10^3）——测试用例的数量。 每个测试用例的第一行包含两个整数 n 和 m（2 ≤ n ≤ 10^4，n-1 ≤ m ≤ min(10^4, n(n - 1)/2)）——顶点的数量和边的数量。 接下来的 m 行包含边的描述，每行两个整数 u 和 v（1 ≤ u, v ≤ n，u ≠ v）——由边连接的顶点的索引。保证任意两个顶点之间最多有一条边（即图中没有多条边）。 然后是一行包含数字 f（1 ≤ f ≤ 10^4）——Kirill 的朋友的数量。 接下来的一行包含 f 个整数：h_1, h_2, ..., h_f（2 ≤ h_i ≤ n）——他们居住的顶点。可能有重复的顶点。 接下来的一行包含数字 k（1 ≤ k ≤ min(6, f)）——没有车的朋友的数量。 每个测试用例的最后一行包含 k 个整数：p_1, p_2, ..., p_k（1 ≤ p_i ≤ f，p_i < p_{i+1}）——没有车的朋友的索引。 保证所有案例的 n 之和不超过 10^4，m 和 f 的总和也是如此。 输出格式： 输出 t 行，每行包含对应测试用例的答案。作为答案，输出一个整数——将不得不步行的朋友的最小可能数量。 输入输出样例： 输入样例 #1： 3 6 7 1 2 2 3 2 4 3 5 4 5 3 6 6 5 5 2 3 4 5 6 4 1 2 3 5 6 7 1 2 2 3 2 4 3 5 4 5 3 6 6 5 6 2 3 4 5 6 5 4 1 2 3 5 4 4 1 2 1 3 2 3 3 4 3 3 4 2 2 1 3 输出样例 #1： 2 1 1 输入样例 #2： 3 2 1 1 2 3 2 2 2 3 1 2 3 3 3 1 2 1 3 2 3 4 2 2 2 3 3 1 2 4 4 4 3 1 3 2 1 4 2 4 5 3 2 2 4 2 3 1 3 4 输出样例 #2： 3 1 0