309829: CF1741F. Multi-Colored Segments
Memory Limit:256 MB
Time Limit:3 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Multi-Colored Segments
题意翻译
给定一维数轴上 $n$ 条线段,每条线段都有给定的颜色 $c_i$。 对于每个 $i$,请求出: $$\min_{c_j\ne c_i}dis(i,j)$$ 其中 $dis(i,j)$ 表示线段 $i,j$ 之间的距离,特别地,有相交(包括端点)的两条线段之间的距离定义为 $0$。 $T$ 组询问,$\sum n \leq 2\times 10^5$,线段两端点 $1\leq l,r \leq 10^9,1\leq c\leq n$。题目描述
Dmitry has $ n $ segments of different colors on the coordinate axis $ Ox $ . Each segment is characterized by three integers $ l_i $ , $ r_i $ and $ c_i $ ( $ 1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n $ ), where $ l_i $ and $ r_i $ are are the coordinates of the ends of the $ i $ -th segment, and $ c_i $ is its color. Dmitry likes to find the minimum distances between segments. However, he considers pairs of segments of the same color uninteresting. Therefore, he wants to know for each segment the distance from this segment to the nearest differently colored segment. The distance between two segments is the minimum of the distances between a point of the first segment and a point of the second segment. In particular, if the segments intersect, then the distance between them is equal to $ 0 $ . For example, Dmitry has $ 5 $ segments: 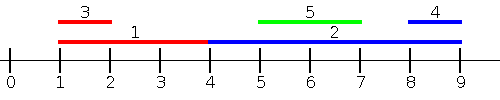- The first segment intersects with the second (and these are segments of different colors), so the answers for them are equal to $ 0 $ . - For the $ 3 $ -rd segment, the nearest segment of a different color is the $ 2 $ -nd segment, the distance to which is equal to $ 2 $ . - For the $ 4 $ -th segment, the nearest segment of a different color is the $ 5 $ -th segment, the distance to which is equal to $ 1 $ . - The $ 5 $ -th segment lies inside the $ 2 $ -nd segment (and these are segments of different colors), so the answers for them are equal to $ 0 $ .输入输出格式
输入格式
The first line of the input contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases in the test. The descriptions of the test cases follow. The first line of description of each test case contains one integer $ n $ ( $ 2 \le n \le 2 \cdot 10^5 $ ) — the number of segments. The next $ n $ lines contain descriptions of the segments. Each segment is described by three integers $ l_i $ , $ r_i $ and $ c_i $ ( $ 1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n $ ) — coordinates of the left and right ends of $ i $ -th segment, as well as the color of this segment. It is guaranteed that there are at least $ 2 $ segments of different colors. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .
输出格式
For each test case, on a separate line print $ n $ integers, where the $ i $ -th number is equal to the distance from the $ i $ -th segment to the nearest segment of a different color.
输入输出样例
输入样例 #1
9
3
1 2 1
3 4 1
5 6 2
2
100000000 200000000 1
900000000 1000000000 2
5
1 2 1
2 3 2
3 4 3
4 5 4
5 6 5
5
1 5 1
4 9 2
1 2 1
8 9 2
5 7 3
2
1 100 2
10 90 1
3
1 1 1
10 10 2
1000000000 1000000000 3
3
3 4 1
2 5 1
1 6 2
6
5 6 2
11 12 3
7 8 2
3 4 2
1 2 1
9 10 2
2
1 3 1
2 3 2输出样例 #1
3 1 1
700000000 700000000
0 0 0 0 0
0 0 2 1 0
0 0
9 9 999999990
0 0 0
3 1 3 1 1 1
0 0输入样例 #2
4
8
11 16 7
12 15 7
2 5 8
17 22 5
1 8 8
19 23 8
16 16 6
6 7 5
9
1 4 3
5 11 1
8 11 3
1 10 1
2 11 1
1 10 4
3 11 1
5 7 1
1 11 1
9
25 25 1
26 26 1
24 24 2
13 14 2
12 16 2
17 18 1
19 19 1
24 27 2
24 27 1
9
15 18 1
20 22 2
13 22 2
13 22 2
3 13 2
6 10 2
3 6 2
19 24 2
22 24 2输出样例 #2
0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 3 1 1 3 0 0
0 2 0 0 2 5 9 1 4说明
In the first test case of the first sample there is only one segment of color $ 2 $ , and all other segments have color $ 1 $ . Therefore, for segments of color $ 1 $ , the answer is equal to the distance to the $ 3 $ rd segment, and for $ 3 $ rd one, the answer is equal to the minimum of the distances to segments of color $ 1 $ . In the second test case of the first sample there are only $ 2 $ segments, and for both of them the answer is equal to the distance between them. In the third test case of the first sample, each segment intersects at least one of its ends with a segment of a different color, so all answers are equal to $ 0 $ . The fourth test case of the first sample is described in the problem statement. In the fifth test case of the first sample, one segment lies completely inside the other, and for both of them the answer is $ 0 $ . In the sixth test case of the first sample, all segments are points of different colors.Input
题意翻译
给定一维数轴上 $n$ 条线段,每条线段都有给定的颜色 $c_i$。 对于每个 $i$,请求出: $$\min_{c_j\ne c_i}dis(i,j)$$ 其中 $dis(i,j)$ 表示线段 $i,j$ 之间的距离,特别地,有相交(包括端点)的两条线段之间的距离定义为 $0$。 $T$ 组询问,$\sum n \leq 2\times 10^5$,线段两端点 $1\leq l,r \leq 10^9,1\leq c\leq n$。Output
**多色线段**
**题意翻译**
给定一维数轴上的 $n$ 条线段,每条线段都有给定的颜色 $c_i$。
对于每个 $i$,请求出:
$$\min_{c_j\ne c_i}dis(i,j)$$
其中 $dis(i,j)$ 表示线段 $i,j$ 之间的距离,特别地,有相交(包括端点)的两条线段之间的距离定义为 $0$。
$T$ 组询问,$\sum n \leq 2\times 10^5$,线段两端点 $1\leq l,r \leq 10^9,1\leq c\leq n$。
**题目描述**
Dmitry 在坐标轴 $Ox$ 上有 $n$ 条不同颜色的线段。每条线段由三个整数 $l_i$,$r_i$ 和 $c_i$($1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n$)描述,其中 $l_i$ 和 $r_i$ 是第 $i$ 条线段的端点坐标,$c_i$ 是其颜色。
Dmitry 喜欢寻找线段之间的最小距离。然而,他认为相同颜色的线段之间没有意思。因此,他想知道每条线段与最近的颜色不同的线段之间的距离。
两条线段之间的距离是一个线段上的点到另一个线段上的点的最小距离。特别是,如果线段相交,则它们之间的距离等于 $0$。
例如,Dmitry 有 $5$ 条线段:
- 第一条线段与第二条线段相交(且颜色不同),所以它们的答案都是 $0$。
- 对于第三条线段,最近的颜色不同的线段是第二条线段,距离为 $2$。
- 对于第四条线段,最近的颜色不同的线段是第五条线段,距离为 $1$。
- 第五条线段位于第二条线段内(且颜色不同),所以它们的答案都是 $0$。
**输入输出格式**
**输入格式**
输入的第一行包含一个整数 $t$($1 \le t \le 10^4$)——测试用例的数量。
接下来是每个测试用例的描述。
每个测试用例的第一行包含一个整数 $n$($2 \le n \le 2 \cdot 10^5$)——线段的数量。
接下来的 $n$ 行包含线段的描述。每条线段由三个整数 $l_i$,$r_i$ 和 $c_i$($1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n$)描述——第 $i$ 条线段的左右端点坐标以及这条线段的颜色。保证至少有 $2$ 条不同颜色的线段。
保证所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。
**输出格式**
对于每个测试用例,在一行中输出 $n$ 个整数,其中第 $i$ 个数表示第 $i$ 条线段与最近的颜色不同的线段之间的距离。
**输入输出样例**
**输入样例 #1**
```
9
3
1 2 1
3 4 1
5 6 2
2
100000000 200000000 1
900000000 1000000000 2
5
1 2 1
2 3 2
3 4 3
4 5 4
5 6 5
5
1 5 1
4 9 2
1 2 1
8 9 2
5 7 3
2
1 100 2
10 90 1
3
1 1 1
10 10 2
1000000000 1000000000 3
3
3 4 1
2 5 1
1 6 2
6
5 6 2
11 12 3
7 8 2
3 4 2
1 2 1
9 10 2
2
1 3 1
2 3 2
```
**输出样例 #1**
```
3 1 1
700000000 700000000
0 0 0 0 0
0 0 2 1 0
0 0
9 9 999999990
0 0 0
3 1 3 1 1 1
0 0
```
**输入样例 #2**
```
4
8
11 16 7
12 15 7**多色线段** **题意翻译** 给定一维数轴上的 $n$ 条线段,每条线段都有给定的颜色 $c_i$。 对于每个 $i$,请求出: $$\min_{c_j\ne c_i}dis(i,j)$$ 其中 $dis(i,j)$ 表示线段 $i,j$ 之间的距离,特别地,有相交(包括端点)的两条线段之间的距离定义为 $0$。 $T$ 组询问,$\sum n \leq 2\times 10^5$,线段两端点 $1\leq l,r \leq 10^9,1\leq c\leq n$。 **题目描述** Dmitry 在坐标轴 $Ox$ 上有 $n$ 条不同颜色的线段。每条线段由三个整数 $l_i$,$r_i$ 和 $c_i$($1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n$)描述,其中 $l_i$ 和 $r_i$ 是第 $i$ 条线段的端点坐标,$c_i$ 是其颜色。 Dmitry 喜欢寻找线段之间的最小距离。然而,他认为相同颜色的线段之间没有意思。因此,他想知道每条线段与最近的颜色不同的线段之间的距离。 两条线段之间的距离是一个线段上的点到另一个线段上的点的最小距离。特别是,如果线段相交,则它们之间的距离等于 $0$。 例如,Dmitry 有 $5$ 条线段: - 第一条线段与第二条线段相交(且颜色不同),所以它们的答案都是 $0$。 - 对于第三条线段,最近的颜色不同的线段是第二条线段,距离为 $2$。 - 对于第四条线段,最近的颜色不同的线段是第五条线段,距离为 $1$。 - 第五条线段位于第二条线段内(且颜色不同),所以它们的答案都是 $0$。 **输入输出格式** **输入格式** 输入的第一行包含一个整数 $t$($1 \le t \le 10^4$)——测试用例的数量。 接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$($2 \le n \le 2 \cdot 10^5$)——线段的数量。 接下来的 $n$ 行包含线段的描述。每条线段由三个整数 $l_i$,$r_i$ 和 $c_i$($1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n$)描述——第 $i$ 条线段的左右端点坐标以及这条线段的颜色。保证至少有 $2$ 条不同颜色的线段。 保证所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。 **输出格式** 对于每个测试用例,在一行中输出 $n$ 个整数,其中第 $i$ 个数表示第 $i$ 条线段与最近的颜色不同的线段之间的距离。 **输入输出样例** **输入样例 #1** ``` 9 3 1 2 1 3 4 1 5 6 2 2 100000000 200000000 1 900000000 1000000000 2 5 1 2 1 2 3 2 3 4 3 4 5 4 5 6 5 5 1 5 1 4 9 2 1 2 1 8 9 2 5 7 3 2 1 100 2 10 90 1 3 1 1 1 10 10 2 1000000000 1000000000 3 3 3 4 1 2 5 1 1 6 2 6 5 6 2 11 12 3 7 8 2 3 4 2 1 2 1 9 10 2 2 1 3 1 2 3 2 ``` **输出样例 #1** ``` 3 1 1 700000000 700000000 0 0 0 0 0 0 0 2 1 0 0 0 9 9 999999990 0 0 0 3 1 3 1 1 1 0 0 ``` **输入样例 #2** ``` 4 8 11 16 7 12 15 7
**题意翻译**
给定一维数轴上的 $n$ 条线段,每条线段都有给定的颜色 $c_i$。
对于每个 $i$,请求出:
$$\min_{c_j\ne c_i}dis(i,j)$$
其中 $dis(i,j)$ 表示线段 $i,j$ 之间的距离,特别地,有相交(包括端点)的两条线段之间的距离定义为 $0$。
$T$ 组询问,$\sum n \leq 2\times 10^5$,线段两端点 $1\leq l,r \leq 10^9,1\leq c\leq n$。
**题目描述**
Dmitry 在坐标轴 $Ox$ 上有 $n$ 条不同颜色的线段。每条线段由三个整数 $l_i$,$r_i$ 和 $c_i$($1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n$)描述,其中 $l_i$ 和 $r_i$ 是第 $i$ 条线段的端点坐标,$c_i$ 是其颜色。
Dmitry 喜欢寻找线段之间的最小距离。然而,他认为相同颜色的线段之间没有意思。因此,他想知道每条线段与最近的颜色不同的线段之间的距离。
两条线段之间的距离是一个线段上的点到另一个线段上的点的最小距离。特别是,如果线段相交,则它们之间的距离等于 $0$。
例如,Dmitry 有 $5$ 条线段:
- 第一条线段与第二条线段相交(且颜色不同),所以它们的答案都是 $0$。
- 对于第三条线段,最近的颜色不同的线段是第二条线段,距离为 $2$。
- 对于第四条线段,最近的颜色不同的线段是第五条线段,距离为 $1$。
- 第五条线段位于第二条线段内(且颜色不同),所以它们的答案都是 $0$。
**输入输出格式**
**输入格式**
输入的第一行包含一个整数 $t$($1 \le t \le 10^4$)——测试用例的数量。
接下来是每个测试用例的描述。
每个测试用例的第一行包含一个整数 $n$($2 \le n \le 2 \cdot 10^5$)——线段的数量。
接下来的 $n$ 行包含线段的描述。每条线段由三个整数 $l_i$,$r_i$ 和 $c_i$($1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n$)描述——第 $i$ 条线段的左右端点坐标以及这条线段的颜色。保证至少有 $2$ 条不同颜色的线段。
保证所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。
**输出格式**
对于每个测试用例,在一行中输出 $n$ 个整数,其中第 $i$ 个数表示第 $i$ 条线段与最近的颜色不同的线段之间的距离。
**输入输出样例**
**输入样例 #1**
```
9
3
1 2 1
3 4 1
5 6 2
2
100000000 200000000 1
900000000 1000000000 2
5
1 2 1
2 3 2
3 4 3
4 5 4
5 6 5
5
1 5 1
4 9 2
1 2 1
8 9 2
5 7 3
2
1 100 2
10 90 1
3
1 1 1
10 10 2
1000000000 1000000000 3
3
3 4 1
2 5 1
1 6 2
6
5 6 2
11 12 3
7 8 2
3 4 2
1 2 1
9 10 2
2
1 3 1
2 3 2
```
**输出样例 #1**
```
3 1 1
700000000 700000000
0 0 0 0 0
0 0 2 1 0
0 0
9 9 999999990
0 0 0
3 1 3 1 1 1
0 0
```
**输入样例 #2**
```
4
8
11 16 7
12 15 7**多色线段** **题意翻译** 给定一维数轴上的 $n$ 条线段,每条线段都有给定的颜色 $c_i$。 对于每个 $i$,请求出: $$\min_{c_j\ne c_i}dis(i,j)$$ 其中 $dis(i,j)$ 表示线段 $i,j$ 之间的距离,特别地,有相交(包括端点)的两条线段之间的距离定义为 $0$。 $T$ 组询问,$\sum n \leq 2\times 10^5$,线段两端点 $1\leq l,r \leq 10^9,1\leq c\leq n$。 **题目描述** Dmitry 在坐标轴 $Ox$ 上有 $n$ 条不同颜色的线段。每条线段由三个整数 $l_i$,$r_i$ 和 $c_i$($1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n$)描述,其中 $l_i$ 和 $r_i$ 是第 $i$ 条线段的端点坐标,$c_i$ 是其颜色。 Dmitry 喜欢寻找线段之间的最小距离。然而,他认为相同颜色的线段之间没有意思。因此,他想知道每条线段与最近的颜色不同的线段之间的距离。 两条线段之间的距离是一个线段上的点到另一个线段上的点的最小距离。特别是,如果线段相交,则它们之间的距离等于 $0$。 例如,Dmitry 有 $5$ 条线段: - 第一条线段与第二条线段相交(且颜色不同),所以它们的答案都是 $0$。 - 对于第三条线段,最近的颜色不同的线段是第二条线段,距离为 $2$。 - 对于第四条线段,最近的颜色不同的线段是第五条线段,距离为 $1$。 - 第五条线段位于第二条线段内(且颜色不同),所以它们的答案都是 $0$。 **输入输出格式** **输入格式** 输入的第一行包含一个整数 $t$($1 \le t \le 10^4$)——测试用例的数量。 接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$($2 \le n \le 2 \cdot 10^5$)——线段的数量。 接下来的 $n$ 行包含线段的描述。每条线段由三个整数 $l_i$,$r_i$ 和 $c_i$($1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n$)描述——第 $i$ 条线段的左右端点坐标以及这条线段的颜色。保证至少有 $2$ 条不同颜色的线段。 保证所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。 **输出格式** 对于每个测试用例,在一行中输出 $n$ 个整数,其中第 $i$ 个数表示第 $i$ 条线段与最近的颜色不同的线段之间的距离。 **输入输出样例** **输入样例 #1** ``` 9 3 1 2 1 3 4 1 5 6 2 2 100000000 200000000 1 900000000 1000000000 2 5 1 2 1 2 3 2 3 4 3 4 5 4 5 6 5 5 1 5 1 4 9 2 1 2 1 8 9 2 5 7 3 2 1 100 2 10 90 1 3 1 1 1 10 10 2 1000000000 1000000000 3 3 3 4 1 2 5 1 1 6 2 6 5 6 2 11 12 3 7 8 2 3 4 2 1 2 1 9 10 2 2 1 3 1 2 3 2 ``` **输出样例 #1** ``` 3 1 1 700000000 700000000 0 0 0 0 0 0 0 2 1 0 0 0 9 9 999999990 0 0 0 3 1 3 1 1 1 0 0 ``` **输入样例 #2** ``` 4 8 11 16 7 12 15 7