309731: CF1726C. Jatayu's Balanced Bracket Sequence
Memory Limit:256 MB
Time Limit:2 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Jatayu's Balanced Bracket Sequence
题意翻译
### 题目大意 对于一个长度为 $2n$ 的**合法**的括号串 $s$,按照如下方法构造一张无向图: - 括号序列的所有位置都是无向图中的一个点。 - 对于该序列的任意位置 $l$,它能向另一个位置 $r$ 连边当且仅当满足子串 $s[l, \; \dots , \; r]$ 也是一个**合法**括号串。 求这张无向图的连通块个数。 ### 输入格式 第一行包含一个整数 $T \; (1 \leqslant T \leqslant 10^5)$ 表示测试样例组数。 对于每组测试样例,第一行包含一个整数 $n \; (1 \leqslant n \leqslant 10^5)$ 表示序列长度为 $2n$。 接下来的一行包含一个长度为 $2n$ 的合法括号串。 ### 输出格式 对于每组测试样例,包含一个整数表示该串构造的无向图的连通块数。 $Translated \; by \; Zigh$题目描述
Last summer, Feluda gifted Lalmohan-Babu a balanced bracket sequence $ s $ of length $ 2 n $ . Topshe was bored during his summer vacations, and hence he decided to draw an undirected graph of $ 2 n $ vertices using the balanced bracket sequence $ s $ . For any two distinct vertices $ i $ and $ j $ ( $ 1 \le i < j \le 2 n $ ), Topshe draws an edge (undirected and unweighted) between these two nodes if and only if the subsegment $ s[i \ldots j] $ forms a balanced bracket sequence. Determine the number of connected components in Topshe's graph. See the Notes section for definitions of the underlined terms.输入输出格式
输入格式
Each test contains multiple test cases. The first line contains a single integer $ t $ ( $ 1 \le t \le 10^5 $ ) — the number of test cases. Description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 10^5 $ ) — the number of opening brackets in string $ s $ . The second line of each test case contains a string $ s $ of length $ 2 n $ — a balanced bracket sequence consisting of $ n $ opening brackets "(", and $ n $ closing brackets ")". It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^5 $ .
输出格式
For each test case, output a single integer — the number of connected components in Topshe's graph.
输入输出样例
输入样例 #1
4
1
()
3
()(())
3
((()))
4
(())(())输出样例 #1
1
2
3
3说明
Sample explanation: In the first test case, the graph constructed from the bracket sequence (), is just a graph containing nodes $ 1 $ and $ 2 $ connected by a single edge. In the second test case, the graph constructed from the bracket sequence ()(()) would be the following (containing two connected components): 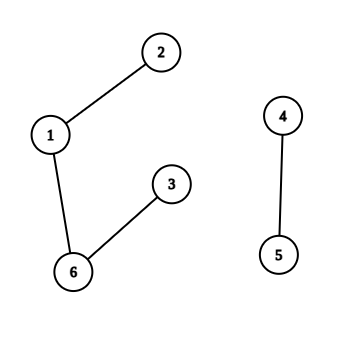Definition of Underlined Terms: - A sequence of brackets is called balanced if one can turn it into a valid math expression by adding characters $ + $ and $ 1 $ . For example, sequences (())(), (), and (()(())) are balanced, while )(, ((), and (()))( are not. - The subsegment $ s[l \ldots r] $ denotes the sequence $ [s_l, s_{l + 1}, \ldots, s_r] $ . - A connected component is a set of vertices $ X $ such that for every two vertices from this set there exists at least one path in the graph connecting these vertices, but adding any other vertex to $ X $ violates this rule.Input
题意翻译
### 题目大意 对于一个长度为 $2n$ 的**合法**的括号串 $s$,按照如下方法构造一张无向图: - 括号序列的所有位置都是无向图中的一个点。 - 对于该序列的任意位置 $l$,它能向另一个位置 $r$ 连边当且仅当满足子串 $s[l, \; \dots , \; r]$ 也是一个**合法**括号串。 求这张无向图的连通块个数。 ### 输入格式 第一行包含一个整数 $T \; (1 \leqslant T \leqslant 10^5)$ 表示测试样例组数。 对于每组测试样例,第一行包含一个整数 $n \; (1 \leqslant n \leqslant 10^5)$ 表示序列长度为 $2n$。 接下来的一行包含一个长度为 $2n$ 的合法括号串。 ### 输出格式 对于每组测试样例,包含一个整数表示该串构造的无向图的连通块数。 $Translated \; by \; Zigh$Output
**Jatayu's Balanced Bracket Sequence**
**题目大意**
对于一个长度为 $2n$ 的**合法**的括号串 $s$,可以构造一张无向图:
- 括号序列的每个位置都是图中的一个顶点。
- 序列中任意位置 $l$ 能与另一个位置 $r$ 连接一条边当且仅当子串 $s[l, \; \dots , \; r]$ 也是一个**合法**括号串。
求这张无向图的连通块个数。
**输入格式**
第一行包含一个整数 $T \; (1 \leqslant T \leqslant 10^5)$ 表示测试样例组数。
每组测试样例,第一行包含一个整数 $n \; (1 \leqslant n \leqslant 10^5)$ 表示序列长度为 $2n$。
接下来的一行包含一个长度为 $2n$ 的合法括号串。
**输出格式**
对于每组测试样例,输出一个整数表示该串构造的无向图的连通块数。
**题目描述**
去年夏天,Feluda送给Lalmohan-Babu一个长度为 $2n$ 的平衡括号序列 $s$。
Topshe在暑假期间感到无聊,因此他决定使用平衡括号序列 $s$ 绘制一个 $2n$ 个顶点的无向图。对于任意两个不同的顶点 $i$ 和 $j$ ($1 \le i < j \le 2n$),如果子段 $s[i \ldots j]$ 形成一个平衡括号序列,Topshe会在它们之间画一条边(无向且未加权)。
确定Topshe的图中有多少个连通分量。
**输入输出格式**
**输入格式**
每个测试包含多个测试用例。第一行包含一个整数 $t$ ($1 \le t \le 10^5$) — 测试用例的数量。接下来是测试用例的描述。
每个测试用例的第一行包含一个整数 $n$ ($1 \le n \le 10^5$) — 字符串 $s$ 中的开括号数量。
每个测试用例的第二行包含一个长度为 $2n$ 的字符串 $s$ — 由 $n$ 个开括号 "(" 和 $n$ 个闭括号 ")" 组成的平衡括号序列。
保证所有测试用例中 $n$ 的总和不超过 $10^5$。
**输出格式**
对于每个测试用例,输出一个整数 — Topshe的图中的连通分量数量。
**输入输出样例**
**输入样例 #1**
```
4
1
()
3
()(())
3
((()))
4
(())(())
**输出样例 #1**
```
1
2
3
3
**说明**
示例解释:
在第一个测试用例中,由括号序列 () 构造的图只包含通过一条边连接的节点 $1$ 和 $2$。
在第二个测试用例中,由括号序列 ()(()) 构造的图如下(包含两个连通分量):

**下划线术语的定义**:
- 如果可以通过添加字符 $+$ 和 $1$ 将括号序列转换为有效的数学表达式,则该序列称为平衡的。例如,序列 (())(), (),和 (()(())) 是平衡的,而 )(), ((), 和 (()))( 不是。
- 子段 $s[l \ldots r]$ 表示序列 $[s_l, s_{l + 1}, \ldots, s_r]$。
- 如果对于集合中的任意两个顶点都存在至少一条路径在图中连接这些顶点,但添加任何其他顶点都会违反此规则,则这样的顶点集合称为连通分量。**Jatayu's Balanced Bracket Sequence** **题目大意** 对于一个长度为 $2n$ 的**合法**的括号串 $s$,可以构造一张无向图: - 括号序列的每个位置都是图中的一个顶点。 - 序列中任意位置 $l$ 能与另一个位置 $r$ 连接一条边当且仅当子串 $s[l, \; \dots , \; r]$ 也是一个**合法**括号串。 求这张无向图的连通块个数。 **输入格式** 第一行包含一个整数 $T \; (1 \leqslant T \leqslant 10^5)$ 表示测试样例组数。 每组测试样例,第一行包含一个整数 $n \; (1 \leqslant n \leqslant 10^5)$ 表示序列长度为 $2n$。 接下来的一行包含一个长度为 $2n$ 的合法括号串。 **输出格式** 对于每组测试样例,输出一个整数表示该串构造的无向图的连通块数。 **题目描述** 去年夏天,Feluda送给Lalmohan-Babu一个长度为 $2n$ 的平衡括号序列 $s$。 Topshe在暑假期间感到无聊,因此他决定使用平衡括号序列 $s$ 绘制一个 $2n$ 个顶点的无向图。对于任意两个不同的顶点 $i$ 和 $j$ ($1 \le i < j \le 2n$),如果子段 $s[i \ldots j]$ 形成一个平衡括号序列,Topshe会在它们之间画一条边(无向且未加权)。 确定Topshe的图中有多少个连通分量。 **输入输出格式** **输入格式** 每个测试包含多个测试用例。第一行包含一个整数 $t$ ($1 \le t \le 10^5$) — 测试用例的数量。接下来是测试用例的描述。 每个测试用例的第一行包含一个整数 $n$ ($1 \le n \le 10^5$) — 字符串 $s$ 中的开括号数量。 每个测试用例的第二行包含一个长度为 $2n$ 的字符串 $s$ — 由 $n$ 个开括号 "(" 和 $n$ 个闭括号 ")" 组成的平衡括号序列。 保证所有测试用例中 $n$ 的总和不超过 $10^5$。 **输出格式** 对于每个测试用例,输出一个整数 — Topshe的图中的连通分量数量。 **输入输出样例** **输入样例 #1** ``` 4 1 () 3 ()(()) 3 ((())) 4 (())(()) **输出样例 #1** ``` 1 2 3 3 **说明** 示例解释: 在第一个测试用例中,由括号序列 () 构造的图只包含通过一条边连接的节点 $1$ 和 $2$。 在第二个测试用例中,由括号序列 ()(()) 构造的图如下(包含两个连通分量):  **下划线术语的定义**: - 如果可以通过添加字符 $+$ 和 $1$ 将括号序列转换为有效的数学表达式,则该序列称为平衡的。例如,序列 (())(), (),和 (()(())) 是平衡的,而 )(), ((), 和 (()))( 不是。 - 子段 $s[l \ldots r]$ 表示序列 $[s_l, s_{l + 1}, \ldots, s_r]$。 - 如果对于集合中的任意两个顶点都存在至少一条路径在图中连接这些顶点,但添加任何其他顶点都会违反此规则,则这样的顶点集合称为连通分量。
**题目大意**
对于一个长度为 $2n$ 的**合法**的括号串 $s$,可以构造一张无向图:
- 括号序列的每个位置都是图中的一个顶点。
- 序列中任意位置 $l$ 能与另一个位置 $r$ 连接一条边当且仅当子串 $s[l, \; \dots , \; r]$ 也是一个**合法**括号串。
求这张无向图的连通块个数。
**输入格式**
第一行包含一个整数 $T \; (1 \leqslant T \leqslant 10^5)$ 表示测试样例组数。
每组测试样例,第一行包含一个整数 $n \; (1 \leqslant n \leqslant 10^5)$ 表示序列长度为 $2n$。
接下来的一行包含一个长度为 $2n$ 的合法括号串。
**输出格式**
对于每组测试样例,输出一个整数表示该串构造的无向图的连通块数。
**题目描述**
去年夏天,Feluda送给Lalmohan-Babu一个长度为 $2n$ 的平衡括号序列 $s$。
Topshe在暑假期间感到无聊,因此他决定使用平衡括号序列 $s$ 绘制一个 $2n$ 个顶点的无向图。对于任意两个不同的顶点 $i$ 和 $j$ ($1 \le i < j \le 2n$),如果子段 $s[i \ldots j]$ 形成一个平衡括号序列,Topshe会在它们之间画一条边(无向且未加权)。
确定Topshe的图中有多少个连通分量。
**输入输出格式**
**输入格式**
每个测试包含多个测试用例。第一行包含一个整数 $t$ ($1 \le t \le 10^5$) — 测试用例的数量。接下来是测试用例的描述。
每个测试用例的第一行包含一个整数 $n$ ($1 \le n \le 10^5$) — 字符串 $s$ 中的开括号数量。
每个测试用例的第二行包含一个长度为 $2n$ 的字符串 $s$ — 由 $n$ 个开括号 "(" 和 $n$ 个闭括号 ")" 组成的平衡括号序列。
保证所有测试用例中 $n$ 的总和不超过 $10^5$。
**输出格式**
对于每个测试用例,输出一个整数 — Topshe的图中的连通分量数量。
**输入输出样例**
**输入样例 #1**
```
4
1
()
3
()(())
3
((()))
4
(())(())
**输出样例 #1**
```
1
2
3
3
**说明**
示例解释:
在第一个测试用例中,由括号序列 () 构造的图只包含通过一条边连接的节点 $1$ 和 $2$。
在第二个测试用例中,由括号序列 ()(()) 构造的图如下(包含两个连通分量):

**下划线术语的定义**:
- 如果可以通过添加字符 $+$ 和 $1$ 将括号序列转换为有效的数学表达式,则该序列称为平衡的。例如,序列 (())(), (),和 (()(())) 是平衡的,而 )(), ((), 和 (()))( 不是。
- 子段 $s[l \ldots r]$ 表示序列 $[s_l, s_{l + 1}, \ldots, s_r]$。
- 如果对于集合中的任意两个顶点都存在至少一条路径在图中连接这些顶点,但添加任何其他顶点都会违反此规则,则这样的顶点集合称为连通分量。**Jatayu's Balanced Bracket Sequence** **题目大意** 对于一个长度为 $2n$ 的**合法**的括号串 $s$,可以构造一张无向图: - 括号序列的每个位置都是图中的一个顶点。 - 序列中任意位置 $l$ 能与另一个位置 $r$ 连接一条边当且仅当子串 $s[l, \; \dots , \; r]$ 也是一个**合法**括号串。 求这张无向图的连通块个数。 **输入格式** 第一行包含一个整数 $T \; (1 \leqslant T \leqslant 10^5)$ 表示测试样例组数。 每组测试样例,第一行包含一个整数 $n \; (1 \leqslant n \leqslant 10^5)$ 表示序列长度为 $2n$。 接下来的一行包含一个长度为 $2n$ 的合法括号串。 **输出格式** 对于每组测试样例,输出一个整数表示该串构造的无向图的连通块数。 **题目描述** 去年夏天,Feluda送给Lalmohan-Babu一个长度为 $2n$ 的平衡括号序列 $s$。 Topshe在暑假期间感到无聊,因此他决定使用平衡括号序列 $s$ 绘制一个 $2n$ 个顶点的无向图。对于任意两个不同的顶点 $i$ 和 $j$ ($1 \le i < j \le 2n$),如果子段 $s[i \ldots j]$ 形成一个平衡括号序列,Topshe会在它们之间画一条边(无向且未加权)。 确定Topshe的图中有多少个连通分量。 **输入输出格式** **输入格式** 每个测试包含多个测试用例。第一行包含一个整数 $t$ ($1 \le t \le 10^5$) — 测试用例的数量。接下来是测试用例的描述。 每个测试用例的第一行包含一个整数 $n$ ($1 \le n \le 10^5$) — 字符串 $s$ 中的开括号数量。 每个测试用例的第二行包含一个长度为 $2n$ 的字符串 $s$ — 由 $n$ 个开括号 "(" 和 $n$ 个闭括号 ")" 组成的平衡括号序列。 保证所有测试用例中 $n$ 的总和不超过 $10^5$。 **输出格式** 对于每个测试用例,输出一个整数 — Topshe的图中的连通分量数量。 **输入输出样例** **输入样例 #1** ``` 4 1 () 3 ()(()) 3 ((())) 4 (())(()) **输出样例 #1** ``` 1 2 3 3 **说明** 示例解释: 在第一个测试用例中,由括号序列 () 构造的图只包含通过一条边连接的节点 $1$ 和 $2$。 在第二个测试用例中,由括号序列 ()(()) 构造的图如下(包含两个连通分量):  **下划线术语的定义**: - 如果可以通过添加字符 $+$ 和 $1$ 将括号序列转换为有效的数学表达式,则该序列称为平衡的。例如,序列 (())(), (),和 (()(())) 是平衡的,而 )(), ((), 和 (()))( 不是。 - 子段 $s[l \ldots r]$ 表示序列 $[s_l, s_{l + 1}, \ldots, s_r]$。 - 如果对于集合中的任意两个顶点都存在至少一条路径在图中连接这些顶点,但添加任何其他顶点都会违反此规则,则这样的顶点集合称为连通分量。