Imitating the Key Tree

题意翻译

#### 题目描述 Pak Chanek 有一棵密钥树。这棵树包含 $N$ 个顶点和 $N - 1$ 条边。这些边按照 $1$ 到 $N - 1$ 连接着 $U_i$ 和 $V_i$。最开始，所有边都没有权值。 长度是 $k$ 的路径可以看成这样： $[v_1, e_1, v_2, e_2, v_3, e_3, \ldots, v_k, e_k, v_{k+1}]$ 而且满足以下条件。 - 对于每个 $ i $ , $ v_i $ 是一个顶点且 $ e_i $ 是一条边。 - 对于每个 $ i $ , $ e_i $ 连接了顶点 $ v_i $ 和 $ v_{i+1} $ . 一个环就是一个路径开始和结束顶点相同。 当且仅当路径不多次使用同一条边时，图中的路径称为简单。请注意，简单路径可以多次使用同一顶点。 有权图中简单路径的权重为它所遍历的所有边的最大权重。 要求计算满足以下条件的不同无向带权图的数量： - 图有 $ N $ 个顶点和 $ 2N-2 $ 条边. - 对于每一对顶点 $ (x, y) $ , 一定有一条简单环路通过了 $ x $ 和 $ y $。 - 每条边的权重为 $ 1 $ 到 $ 2N-2 $ 的一个整数，而且每条边的权重不同。 - 该图可以这样的方式生成，即有一种方法将权重 $W_i$ 分配给满足以下条件的密钥树中的每个边$i$： - 对于每一对边 $ (i, j) $ , 如果 $ i<j $ , 那么 $ W_i<W_j $ . - 对于每一对不同的顶点编号 $ (x, y) $ , 从 $ x $ 到 $ y $ 唯一的简单路花费等于通过图中顶点 $x$ 和 $y$ 的简单环路的最小成本。 - **请注意，图可能有重边，但没有自环。** 输出答案对 $998\,244\,353 $ 取模的结果。 当且仅当存在三元组$（a，b，c）$时，两个图被认为是不同的，从而在一个图中存在将顶点$a$和$b$与权重$c$连接的边，而在另一个图上不存在。 #### 输入格式 第一行包含了一个整数 $N$，代表顶点的个数。 接下来 $N - 1$ 行中的第 $i$ 行包含了两个整数 $ U_i $ 和 $ V_i $ ，表示一条连接 $U_i$ 和 $V_i$ 的边。 #### 输出格式 一个整数表示满足问题条件的不同无向带权图的数目对$ 998\,244\,353 $ 取模的结果。 #### 样例 #1 ##### 样例输入 #1 ``` 4 3 2 1 3 4 3 ``` ##### 样例输出 #1 ``` 540 ``` #### 提示 以下是满足条件的图的示例。 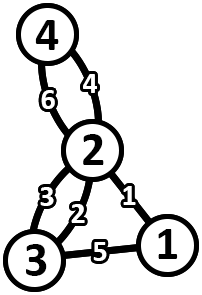 以下是对应于上图的关键树中边权重的分配。 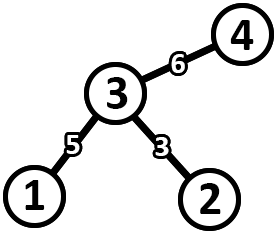 例如，考虑一对顶点索引 $ (1, 4) $ . - 这对顶点的环路是 $ 3 \xrightarrow{2} 2 \xrightarrow{4} 4 \xrightarrow{6} 2 \xrightarrow{1} 1 \xrightarrow{5} 3 $ ，花费为 $ 6 $ . - 这对顶点的路径为： $ 1 \xrightarrow{5} 3 \xrightarrow{6} 4 $ 花费为 $ 6 $ . #### 数据范围 对于 $100\%$ 的样例，$ 2 \le N \le 10^5 ， 1 \le U_i, V_i \le N 。$

题目描述

Pak Chanek has a tree called the key tree. This tree consists of $ N $ vertices and $ N-1 $ edges. The edges of the tree are numbered from $ 1 $ to $ N-1 $ with edge $ i $ connecting vertices $ U_i $ and $ V_i $ . Initially, each edge of the key tree does not have a weight. Formally, a path with length $ k $ in a graph is a sequence $ [v_1, e_1, v_2, e_2, v_3, e_3, \ldots, v_k, e_k, v_{k+1}] $ such that: - For each $ i $ , $ v_i $ is a vertex and $ e_i $ is an edge. - For each $ i $ , $ e_i $ connects vertices $ v_i $ and $ v_{i+1} $ . A circuit is a path that starts and ends on the same vertex. A path in a graph is said to be simple if and only if the path does not use the same edge more than once. Note that a simple path can use the same vertex more than once. The cost of a simple path in a weighted graph is defined as the maximum weight of all edges it traverses. Count the number of distinct undirected weighted graphs that satisfy the following conditions: - The graph has $ N $ vertices and $ 2N-2 $ edges. - For each pair of different vertices $ (x, y) $ , there exists a simple circuit that goes through vertices $ x $ and $ y $ in the graph. - The weight of each edge in the graph is an integer between $ 1 $ and $ 2N-2 $ inclusive. Each edge has distinct weights. - The graph is formed in a way such that there is a way to assign a weight $ W_i $ to each edge $ i $ in the key tree that satisfies the following conditions: - For each pair of edges $ (i, j) $ , if $ i<j $ , then $ W_i<W_j $ . - For each pair of different vertex indices $ (x, y) $ , the cost of the only simple path from vertex $ x $ to $ y $ in the key tree is equal to the minimum cost of a simple circuit that goes through vertices $ x $ and $ y $ in the graph. - Note that the graph is allowed to have multi-edges, but is not allowed to have self-loops. Print the answer modulo $ 998\,244\,353 $ . Two graphs are considered distinct if and only if there exists a triple $ (a, b, c) $ such that there exists an edge that connects vertices $ a $ and $ b $ with weight $ c $ in one graph, but not in the other.

输入输出格式

输入格式

The first line contains a single integer $ N $ ( $ 2 \le N \le 10^5 $ ) — the number of vertices in the key tree. The $ i $ -th of the next $ N-1 $ lines contains two integers $ U_i $ and $ V_i $ ( $ 1 \le U_i, V_i \le N $ ) — an edge connecting vertices $ U_i $ and $ V_i $ . The graph in the input is a tree.

输出格式

An integer representing the number of distinct undirected weighted graphs that satisfy the conditions of the problem modulo $ 998\,244\,353 $ .

输入输出样例

输入样例 #1

4
3 2
1 3
4 3

输出样例 #1

540

说明

The following is an example of a graph that satisfies.  The following is an assignment of edge weights in the key tree that corresponds to the graph above.  As an example, consider a pair of vertex indices $ (1, 4) $ . - The circuit in the graph for this pair of vertices is $ 3 \xrightarrow{2} 2 \xrightarrow{4} 4 \xrightarrow{6} 2 \xrightarrow{1} 1 \xrightarrow{5} 3 $ with a cost of $ 6 $ . - The path in the key tree for this pair of vertices is $ 1 \xrightarrow{5} 3 \xrightarrow{6} 4 $ with a cost of $ 6 $ .

题意翻译

#### 题目描述 Pak Chanek 有一棵密钥树。这棵树包含 $N$ 个顶点和 $N - 1$ 条边。这些边按照 $1$ 到 $N - 1$ 连接着 $U_i$ 和 $V_i$。最开始，所有边都没有权值。 长度是 $k$ 的路径可以看成这样： $[v_1, e_1, v_2, e_2, v_3, e_3, \ldots, v_k, e_k, v_{k+1}]$ 而且满足以下条件。 - 对于每个 $ i $ , $ v_i $ 是一个顶点且 $ e_i $ 是一条边。 - 对于每个 $ i $ , $ e_i $ 连接了顶点 $ v_i $ 和 $ v_{i+1} $ . 一个环就是一个路径开始和结束顶点相同。 当且仅当路径不多次使用同一条边时，图中的路径称为简单。请注意，简单路径可以多次使用同一顶点。 有权图中简单路径的权重为它所遍历的所有边的最大权重。 要求计算满足以下条件的不同无向带权图的数量： - 图有 $ N $ 个顶点和 $ 2N-2 $ 条边. - 对于每一对顶点 $ (x, y) $ , 一定有一条简单环路通过了 $ x $ 和 $ y $。 - 每条边的权重为 $ 1 $ 到 $ 2N-2 $ 的一个整数，而且每条边的权重不同。 - 该图可以这样的方式生成，即有一种方法将权重 $W_i$ 分配给满足以下条件的密钥树中的每个边$i$： - 对于每一对边 $ (i, j) $ , 如果 $ i<j $ , 那么 $ W_i<W_j $ . - 对于每一对不同的顶点编号 $ (x, y) $ , 从 $ x $ 到 $ y $ 唯一的简单路花费等于通过图中顶点 $x$ 和 $y$ 的简单环路的最小成本。 - **请注意，图可能有重边，但没有自环。** 输出答案对 $998\,244\,353 $ 取模的结果。 当且仅当存在三元组$（a，b，c）$时，两个图被认为是不同的，从而在一个图中存在将顶点$a$和$b$与权重$c$连接的边，而在另一个图上不存在。 #### 输入格式 第一行包含了一个整数 $N$，代表顶点的个数。 接下来 $N - 1$ 行中的第 $i$ 行包含了两个整数 $ U_i $ 和 $ V_i $ ，表示一条连接 $U_i$ 和 $V_i$ 的边。 #### 输出格式 一个整数表示满足问题条件的不同无向带权图的数目对$ 998\,244\,353 $ 取模的结果。 #### 样例 #1 ##### 样例输入 #1 ``` 4 3 2 1 3 4 3 ``` ##### 样例输出 #1 ``` 540 ``` #### 提示 以下是满足条件的图的示例。  以下是对应于上图的关键树中边权重的分配。  例如，考虑一对顶点索引 $ (1, 4) $ . - 这对顶点的环路是 $ 3 \xrightarrow{2} 2 \xrightarrow{4} 4 \xrightarrow{6} 2 \xrightarrow{1} 1 \xrightarrow{5} 3 $ ，花费为 $ 6 $ . - 这对顶点的路径为： $ 1 \xrightarrow{5} 3 \xrightarrow{6} 4 $ 花费为 $ 6 $ . #### 数据范围 对于 $100\%$ 的样例，$ 2 \le N \le 10^5 ， 1 \le U_i, V_i \le N 。$