Traveling Salesman Problem

题意翻译

你正位于一个无限的笛卡尔坐标系的点 $ (x , y) $上，你可以进行四种操作： - 向左移动至 $ (x - 1, y) $ - 向右移动至 $ (x + 1, y) $ - 向上移动至 $ (x, y + 1) $ - 向下移动至 $ (x, y - 1) $ 有 $ n $ 个宝箱在这个平面上。 第 $ i $ 个 宝箱的坐标为 $ (x_i,y_i) $ . 保证每个宝箱都在 $ x $ 轴 或 $ y $ 轴上。即 $ x_i=0 $ 或 $ y_i=0 $。 你现在点 $ (0,0) $ 上，想将所有宝箱全部收入囊中，并回到原点。 你想知道你需要的最小移动次数是多少。 本题使用多组测试数据。 **【输入格式】** 第一行包含一个整数 $ t $（$ 1 \le t \le 100 $）— 测试组数 对于每一组数据， 第一行包含一个整数 $ n $（$ 1 \le n \le 100 $）— 宝箱数量 第 $ i+1 $ 行 $ n $ 包含两个整数 $ x_i $ 和 $ y_i $（$ -100 \le x_i, y_i \le 100 $）— 第 $i$ 个宝箱的坐标，保证 $ x_i=0 $ 或 $ y_i=0 $。 注意每一组数据的 $n$ 的和是无限制的 **【输出格式】** 共 $t$ 行，每行包含一个整数，即最小步数

题目描述

You are living on an infinite plane with the Cartesian coordinate system on it. In one move you can go to any of the four adjacent points (left, right, up, down). More formally, if you are standing at the point $ (x, y) $ , you can: - go left, and move to $ (x - 1, y) $ , or - go right, and move to $ (x + 1, y) $ , or - go up, and move to $ (x, y + 1) $ , or - go down, and move to $ (x, y - 1) $ . There are $ n $ boxes on this plane. The $ i $ -th box has coordinates $ (x_i,y_i) $ . It is guaranteed that the boxes are either on the $ x $ -axis or the $ y $ -axis. That is, either $ x_i=0 $ or $ y_i=0 $ . You can collect a box if you and the box are at the same point. Find the minimum number of moves you have to perform to collect all of these boxes if you have to start and finish at the point $ (0,0) $ .

输入输出格式

输入格式

The first line contains a single integer $ t $ ( $ 1 \le t \le 100 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 100 $ ) — the number of boxes. The $ i $ -th line of the following $ n $ lines contains two integers $ x_i $ and $ y_i $ ( $ -100 \le x_i, y_i \le 100 $ ) — the coordinate of the $ i $ -th box. It is guaranteed that either $ x_i=0 $ or $ y_i=0 $ . Do note that the sum of $ n $ over all test cases is not bounded.

输出格式

For each test case output a single integer — the minimum number of moves required.

输入输出样例

输入样例 #1

3
4
0 -2
1 0
-1 0
0 2
3
0 2
-3 0
0 -1
1
0 0

输出样例 #1

12
12
0

说明

In the first test case, a possible sequence of moves that uses the minimum number of moves required is shown below. 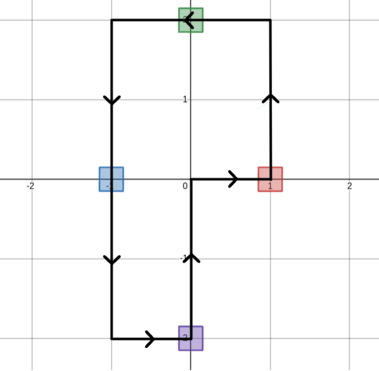 $ $(0,0) \to (1,0) \to (1,1) \to (1, 2) \to (0,2) \to (-1,2) \to (-1,1) \to (-1,0) \to (-1,-1) \to (-1,-2) \to (0,-2) \to (0,-1) \to (0,0) $ $ </span> </center><p>In the second test case, a possible sequence of moves that uses the minimum number of moves required is shown below.</p><center> <img class="tex-graphics" src="https://espresso.codeforces.com/be215267232d4ce410faf437f6516dfc445f4232.png" style="max-width: 100.0%;max-height: 100.0%;" /> <span class="tex-font-size-small"> $ $ (0,0) \to (0,1) \to (0,2) \to (-1, 2) \to (-2,2) \to (-3,2) \to (-3,1) \to (-3,0) \to (-3,-1) \to (-2,-1) \to (-1,-1) \to (0,-1) \to (0,0) $ $In the third test case, we can collect all boxes without making any moves.

**旅行推销员问题**

**题意翻译**

你位于一个无限的笛卡尔坐标系的点 $ (x , y) $ 上，你可以进行四种操作：

- 向左移动至 $ (x - 1, y) $
- 向右移动至 $ (x + 1, y) $
- 向上移动至 $ (x, y + 1) $
- 向下移动至 $ (x, y - 1) $

有 $ n $ 个宝箱在这个平面上。 第 $ i $ 个 宝箱的坐标为 $ (x_i,y_i) $ . 保证每个宝箱都在 $ x $ 轴 或 $ y $ 轴上。即 $ x_i=0 $ 或 $ y_i=0 $。

你现在点 $ (0,0) $ 上，想将所有宝箱全部收入囊中，并回到原点。
你想知道你需要的最小移动次数是多少。
本题使用多组测试数据。

**【输入格式】**

第一行包含一个整数 $ t $（$ 1 \le t \le 100 $）— 测试组数

对于每一组数据，

第一行包含一个整数 $ n $（$ 1 \le n \le 100 $）— 宝箱数量

第 $ i+1 $ 行 $ n $ 包含两个整数 $ x_i $ 和 $ y_i $（$ -100 \le x_i, y_i \le 100 $）— 第 $i$ 个宝箱的坐标，保证 $ x_i=0 $ 或 $ y_i=0 $。

注意每一组数据的 $n$ 的和是无限制的

**【输出格式】**

共 $t$ 行，每行包含一个整数，即最小步数

**题目描述**

你在无限平面上生活，它有笛卡尔坐标系。你可以移动到四个相邻点（左，右，上，下）。

更正式地说，如果你站在点 $ (x, y) $ ，你可以：

- 向左移动，移动到 $ (x - 1, y) $ ，或者
- 向右移动，移动到 $ (x + 1, y) $ ，或者
- 向上移动，移动到 $ (x, y + 1) $ ，或者
- 向下移动，移动到 $ (x, y - 1) $ 。

平面上有 $ n $ 个盒子。第 $ i $ 个盒子的坐标是 $ (x_i,y_i) $ 。保证盒子要么在 $ x $ 轴要么在 $ y $ 轴上。即 $ x_i=0 $ 或 $ y_i=0 $ 。

如果你和盒子在同一位置，你可以收集一个盒子。找出你必须要执行的最小移动次数，以收集所有这些盒子，如果你必须从点 $ (0,0) $ 开始并结束。

**输入输出格式**

**输入格式**

第一行包含一个单独的整数 $ t $ （ $ 1 \le t \le 100 $ ）——测试用例的数量。

每个测试用例的第一行包含一个单独的整数 $ n $ （ $ 1 \le n \le 100 $ ）——盒子的数量。

接下来的 $ n $ 行中的第 $ i $ 行包含两个整数 $ x_i $ 和 $ y_i $ （ $ -100 \le x_i, y_i \le 100 $ ）——第 $ i $ 个盒子的坐标。保证 $ x_i=0 $ 或 $ y_i=0 $ 。

注意，所有测试用例中 $ n $ 的总和是无限制的。

**输出格式**

对于每个测试用例输出一个单独的整数——所需的最小移动次数。

**输入输出样例**

**输入样例 #1**

```
3
4
0 -2
1 0
-1 0
0 2
3
0 2
-3 0
0 -1
1
0 0
```

**输出样例 #1**

```
12
12
0
```

**说明**

在第一个测试用例中，使用所需的最小移动次数的可能移动序列如下所示。

在第二个测试用例中，使用所需的最小移动次数的可能移动序列如下所示。

在第三个测试用例中，我们可以不进行任何移动就收集所有盒子。**旅行推销员问题** **题意翻译** 你位于一个无限的笛卡尔坐标系的点 $ (x , y) $ 上，你可以进行四种操作： - 向左移动至 $ (x - 1, y) $ - 向右移动至 $ (x + 1, y) $ - 向上移动至 $ (x, y + 1) $ - 向下移动至 $ (x, y - 1) $ 有 $ n $ 个宝箱在这个平面上。 第 $ i $ 个 宝箱的坐标为 $ (x_i,y_i) $ . 保证每个宝箱都在 $ x $ 轴 或 $ y $ 轴上。即 $ x_i=0 $ 或 $ y_i=0 $。 你现在点 $ (0,0) $ 上，想将所有宝箱全部收入囊中，并回到原点。 你想知道你需要的最小移动次数是多少。 本题使用多组测试数据。 **【输入格式】** 第一行包含一个整数 $ t $（$ 1 \le t \le 100 $）— 测试组数 对于每一组数据， 第一行包含一个整数 $ n $（$ 1 \le n \le 100 $）— 宝箱数量 第 $ i+1 $ 行 $ n $ 包含两个整数 $ x_i $ 和 $ y_i $（$ -100 \le x_i, y_i \le 100 $）— 第 $i$ 个宝箱的坐标，保证 $ x_i=0 $ 或 $ y_i=0 $。 注意每一组数据的 $n$ 的和是无限制的 **【输出格式】** 共 $t$ 行，每行包含一个整数，即最小步数 **题目描述** 你在无限平面上生活，它有笛卡尔坐标系。你可以移动到四个相邻点（左，右，上，下）。 更正式地说，如果你站在点 $ (x, y) $ ，你可以： - 向左移动，移动到 $ (x - 1, y) $ ，或者 - 向右移动，移动到 $ (x + 1, y) $ ，或者 - 向上移动，移动到 $ (x, y + 1) $ ，或者 - 向下移动，移动到 $ (x, y - 1) $ 。 平面上有 $ n $ 个盒子。第 $ i $ 个盒子的坐标是 $ (x_i,y_i) $ 。保证盒子要么在 $ x $ 轴要么在 $ y $ 轴上。即 $ x_i=0 $ 或 $ y_i=0 $ 。 如果你和盒子在同一位置，你可以收集一个盒子。找出你必须要执行的最小移动次数，以收集所有这些盒子，如果你必须从点 $ (0,0) $ 开始并结束。 **输入输出格式** **输入格式** 第一行包含一个单独的整数 $ t $ （ $ 1 \le t \le 100 $ ）——测试用例的数量。 每个测试用例的第一行包含一个单独的整数 $ n $ （ $ 1 \le n \le 100 $ ）——盒子的数量。 接下来的 $ n $ 行中的第 $ i $ 行包含两个整数 $ x_i $ 和 $ y_i $ （ $ -100 \le x_i, y_i \le 100 $ ）——第 $ i $ 个盒子的坐标。保证 $ x_i=0 $ 或 $ y_i=0 $ 。 注意，所有测试用例中 $ n $ 的总和是无限制的。 **输出格式** 对于每个测试用例输出一个单独的整数——所需的最小移动次数。 **输入输出样例** **输入样例 #1** ``` 3 4 0 -2 1 0 -1 0 0 2 3 0 2 -3 0 0 -1 1 0 0 ``` **输出样例 #1** ``` 12 12 0 ``` **说明** 在第一个测试用例中，使用所需的最小移动次数的可能移动序列如下所示。 在第二个测试用例中，使用所需的最小移动次数的可能移动序列如下所示。 在第三个测试用例中，我们可以不进行任何移动就收集所有盒子。