309635: CF1710D. Recover the Tree
Memory Limit:256 MB
Time Limit:3 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Recover the Tree
题意翻译
你需要根据题目给出的信息构造出一棵树,满足如下条件: 1. 树的节点个数为 $n$。 2. 对于每个区间 $[l,r]$ 给出是或不是连通块。 数据保证有解,$n\leqslant 2000$。 translated by cnyali_zyf题目描述
Rhodoks has a tree with $ n $ vertices, but he doesn't remember its structure. The vertices are indexed from $ 1 $ to $ n $ . A segment $ [l,r] $ ( $ 1 \leq l \leq r \leq n $ ) is good if the vertices with indices $ l $ , $ l + 1 $ , ..., $ r $ form a connected component in Rhodoks' tree. Otherwise, it is bad. For example, if the tree is the one in the picture, then only the segment $ [3,4] $ is bad while all the other segments are good. 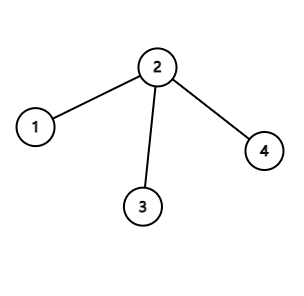For each of the $ \frac{n(n+1)}{2} $ segments, Rhodoks remembers whether it is good or bad. Can you help him recover the tree? If there are multiple solutions, print any. It is guaranteed that the there is at least one tree satisfying Rhodoks' description.输入输出格式
输入格式
Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \leq t \leq 1000 $ ). The description of the test cases follows. The first line of each test case contains an integer $ n $ ( $ 1 \leq n \leq 2000 $ ) — the number of vertices in the tree. Then $ n $ lines follow. The $ i $ -th of these lines contains a string $ good_i $ of length $ n+1-i $ consisting of 0 and 1. If the segment $ [i,i+j-1] $ is good then the $ j $ -th character of $ good_i $ is 1, otherwise $ j $ -th character of $ good_i $ is 0. It is guaranteed that the there is at least one tree consistent with the given data. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2000 $ .
输出格式
For each test case, print $ n-1 $ lines describing the tree you recover. The $ i $ -th line should contain two integers $ u_i $ and $ v_i $ ( $ 1 \leq u_i,v_i \leq n $ ), denoting an edge between vertices $ u_i $ and $ v_i $ . If there are multiple solutions, print any.
输入输出样例
输入样例 #1
3
4
1111
111
10
1
6
111111
11111
1111
111
11
1
12
100100000001
11100000001
1000000000
100000000
10010001
1110000
100000
10000
1001
111
10
1输出样例 #1
1 2
2 3
2 4
1 2
2 3
3 4
4 5
5 6
2 3
6 7
10 11
2 4
6 8
10 12
1 4
5 8
9 12
5 12
2 12说明
The first test case is explained in the statement. In the second test case, one possible tree is as follows: 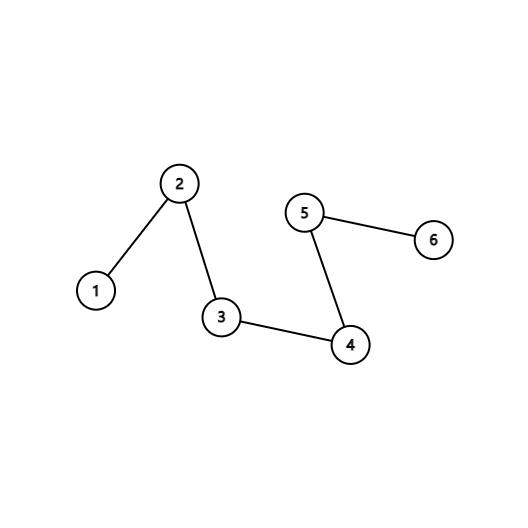In the third test case, one possible tree is as follows: 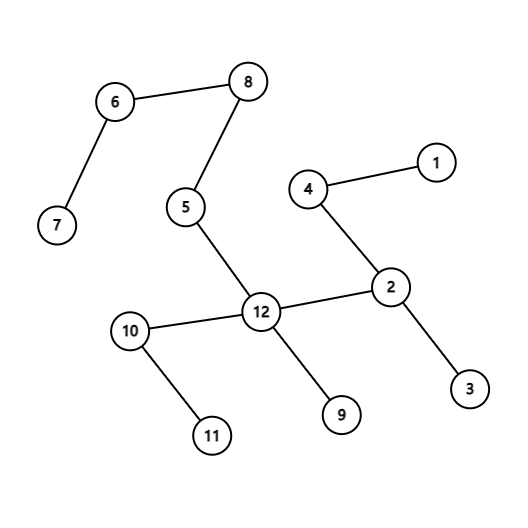Input
题意翻译
你需要根据题目给出的信息构造出一棵树,满足如下条件: 1. 树的节点个数为 $n$。 2. 对于每个区间 $[l,r]$ 给出是或不是连通块。 数据保证有解,$n\leqslant 2000$。 translated by cnyali_zyfOutput
题目大意:
你需要根据题目给出的信息构造出一棵树,满足如下条件:
1. 树的节点个数为 \( n \)。
2. 对于每个区间 \([l,r]\) 给出是或不是连通块。
数据保证有解,\( n \leqslant 2000 \)。
输入输出数据格式:
输入格式:
每个测试包含多个测试案例。第一行包含测试案例的数量 \( t \)(\( 1 \leq t \leq 1000 \))。接下来是测试案例的描述。
每个测试案例的第一行包含一个整数 \( n \)(\( 1 \leq n \leq 2000 \))——树中节点的数量。
然后是 \( n \) 行。第 \( i \) 行包含一个长度为 \( n+1-i \) 的由 0 和 1 组成的字符串 \( good_i \)。如果区间 \([i,i+j-1]\) 是好的,那么 \( good_i \) 的第 \( j \) 个字符是 1,否则是 0。
保证至少存在一个与给定数据一致的树。
保证所有测试案例中 \( n \) 的总和不超过 \( 2000 \)。
输出格式:
对于每个测试案例,打印 \( n-1 \) 行描述你恢复的树。
第 \( i \) 行应包含两个整数 \( u_i \) 和 \( v_i \)(\( 1 \leq u_i,v_i \leq n \)),表示节点 \( u_i \) 和 \( v_i \) 之间的边。
如果有多个解,打印任意一个。题目大意: 你需要根据题目给出的信息构造出一棵树,满足如下条件: 1. 树的节点个数为 \( n \)。 2. 对于每个区间 \([l,r]\) 给出是或不是连通块。 数据保证有解,\( n \leqslant 2000 \)。 输入输出数据格式: 输入格式: 每个测试包含多个测试案例。第一行包含测试案例的数量 \( t \)(\( 1 \leq t \leq 1000 \))。接下来是测试案例的描述。 每个测试案例的第一行包含一个整数 \( n \)(\( 1 \leq n \leq 2000 \))——树中节点的数量。 然后是 \( n \) 行。第 \( i \) 行包含一个长度为 \( n+1-i \) 的由 0 和 1 组成的字符串 \( good_i \)。如果区间 \([i,i+j-1]\) 是好的,那么 \( good_i \) 的第 \( j \) 个字符是 1,否则是 0。 保证至少存在一个与给定数据一致的树。 保证所有测试案例中 \( n \) 的总和不超过 \( 2000 \)。 输出格式: 对于每个测试案例,打印 \( n-1 \) 行描述你恢复的树。 第 \( i \) 行应包含两个整数 \( u_i \) 和 \( v_i \)(\( 1 \leq u_i,v_i \leq n \)),表示节点 \( u_i \) 和 \( v_i \) 之间的边。 如果有多个解,打印任意一个。
你需要根据题目给出的信息构造出一棵树,满足如下条件:
1. 树的节点个数为 \( n \)。
2. 对于每个区间 \([l,r]\) 给出是或不是连通块。
数据保证有解,\( n \leqslant 2000 \)。
输入输出数据格式:
输入格式:
每个测试包含多个测试案例。第一行包含测试案例的数量 \( t \)(\( 1 \leq t \leq 1000 \))。接下来是测试案例的描述。
每个测试案例的第一行包含一个整数 \( n \)(\( 1 \leq n \leq 2000 \))——树中节点的数量。
然后是 \( n \) 行。第 \( i \) 行包含一个长度为 \( n+1-i \) 的由 0 和 1 组成的字符串 \( good_i \)。如果区间 \([i,i+j-1]\) 是好的,那么 \( good_i \) 的第 \( j \) 个字符是 1,否则是 0。
保证至少存在一个与给定数据一致的树。
保证所有测试案例中 \( n \) 的总和不超过 \( 2000 \)。
输出格式:
对于每个测试案例,打印 \( n-1 \) 行描述你恢复的树。
第 \( i \) 行应包含两个整数 \( u_i \) 和 \( v_i \)(\( 1 \leq u_i,v_i \leq n \)),表示节点 \( u_i \) 和 \( v_i \) 之间的边。
如果有多个解,打印任意一个。题目大意: 你需要根据题目给出的信息构造出一棵树,满足如下条件: 1. 树的节点个数为 \( n \)。 2. 对于每个区间 \([l,r]\) 给出是或不是连通块。 数据保证有解,\( n \leqslant 2000 \)。 输入输出数据格式: 输入格式: 每个测试包含多个测试案例。第一行包含测试案例的数量 \( t \)(\( 1 \leq t \leq 1000 \))。接下来是测试案例的描述。 每个测试案例的第一行包含一个整数 \( n \)(\( 1 \leq n \leq 2000 \))——树中节点的数量。 然后是 \( n \) 行。第 \( i \) 行包含一个长度为 \( n+1-i \) 的由 0 和 1 组成的字符串 \( good_i \)。如果区间 \([i,i+j-1]\) 是好的,那么 \( good_i \) 的第 \( j \) 个字符是 1,否则是 0。 保证至少存在一个与给定数据一致的树。 保证所有测试案例中 \( n \) 的总和不超过 \( 2000 \)。 输出格式: 对于每个测试案例,打印 \( n-1 \) 行描述你恢复的树。 第 \( i \) 行应包含两个整数 \( u_i \) 和 \( v_i \)(\( 1 \leq u_i,v_i \leq n \)),表示节点 \( u_i \) 和 \( v_i \) 之间的边。 如果有多个解,打印任意一个。