Subrectangle Guess

题意翻译

## 题目描述 Michael 和 Joe 在玩一个游戏。一共有 $t$ 次，每次 Michael 给出一个 $n\times m$ 的矩阵和一对 $h,w$，Jeo 在 Michael 看不见的情况下盖住任意一个 $h\times w$ 的子矩阵，问 Michael 这个子矩阵中最大的数是多少。Michael 答对即为获胜。 现在，我们对每一次给出的矩阵都要找出一对最小的 $h,w$，使得 Michael 一定能赢。 ## 输入格式 第一行一个整数 $t$，表示有 $t$ 组数据。 接下来对于每一组数据： 第一行两个正整数 $n,m$，表示一个 $n\times m$ 的矩阵。 接下来 $n$ 行，每行 $m$ 个数，表示这个矩阵中的元素。 ## 输出格式 对于每组数据，输出**一个整数**表示我们选出的 $h,w$ **的乘积**。 ### 输入输出样例 #### 样例输入 #1 ```plain 3 1 1 3 4 4 2 12 6 10 3 15 16 4 1 13 8 11 14 7 9 5 2 3 -7 5 2 0 8 -3 ``` #### 样例输出 #1 ```plain 1 9 4 ``` ## 说明/提示 在第一组数据中，矩阵是 $1\times 1$ 的，因此对于 $h,w$，唯一可能的选择是 $h=1，w=1$，给出了 $h\cdot w=1$ 的面积。 描述中展示了第二组数据给出的矩阵。可以证明，只要 $h=3$，$w=3$，迈克尔就能保证胜利，而只要 $h\cdot w\le 8$，任何选择都不能保证胜利。 对于所有数据，$1\le t\le 20,1\le n,m\le 40,-10^9\le 矩阵中的元素\le 10^9$。

题目描述

Michael and Joe are playing a game. The game is played on a grid with $ n $ rows and $ m $ columns, filled with distinct integers. We denote the square on the $ i $ -th ( $ 1\le i\le n $ ) row and $ j $ -th ( $ 1\le j\le m $ ) column by $ (i, j) $ and the number there by $ a_{ij} $ . Michael starts by saying two numbers $ h $ ( $ 1\le h \le n $ ) and $ w $ ( $ 1\le w \le m $ ). Then Joe picks any $ h\times w $ subrectangle of the board (without Michael seeing). Formally, an $ h\times w $ subrectangle starts at some square $ (a,b) $ where $ 1 \le a \le n-h+1 $ and $ 1 \le b \le m-w+1 $ . It contains all squares $ (i,j) $ for $ a \le i \le a+h-1 $ and $ b \le j \le b+w-1 $ . 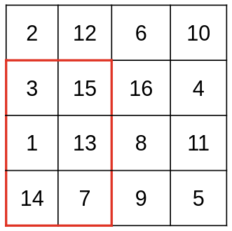Possible move by Joe if Michael says $ 3\times 2 $ (with maximum of $ 15 $ ).Finally, Michael has to guess the maximum number in the subrectangle. He wins if he gets it right. Because Michael doesn't like big numbers, he wants the area of the chosen subrectangle (that is, $ h \cdot w $ ), to be as small as possible, while still ensuring that he wins, not depending on Joe's choice. Help Michael out by finding this minimum possible area. It can be shown that Michael can always choose $ h, w $ for which he can ensure that he wins.

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 20 $ ). Description of the test cases follows. The first line of each test case contains two integers $ n $ and $ m $ ( $ 1 \le n, m \le 40 $ ) — the size of the grid. Each of the following $ n $ lines contains $ m $ integers. The $ j $ -th integer on the $ i $ -th line is $ a_{ij} $ ( $ -10^9 \le a_{ij} \le 10^9 $ ) — the element in the cell $ (i, j) $ . It is guaranteed that all the numbers are distinct (that is, if $ a_{i_1j_1} = a_{i_2j_2} $ , then $ i_1 = i_2, j_1 = j_2 $ ).

输出格式

For each test case print a single positive integer — the minimum possible area the subrectangle can have while still ensuring that Michael can guarantee the victory.

输入输出样例

输入样例 #1

3
1 1
3
4 4
2 12 6 10
3 15 16 4
1 13 8 11
14 7 9 5
2 3
-7 5 2
0 8 -3

输出样例 #1

1
9
4

说明

In the first test case, the grid is $ 1\times 1 $ , so the only possible choice for $ h, w $ is $ h = 1, w = 1 $ , giving an area of $ h\cdot w = 1 $ . The grid from the second test case is drawn in the statement. It can be shown that with $ h = 3, w = 3 $ Michael can guarantee the victory and that any choice with $ h\cdot w \le 8 $ doesn't.

**题意翻译**

Michael 和 Joe 在玩一个游戏。一共有 $ t $ 次，每次 Michael 给出一个 $ n \times m $ 的矩阵和一对 $ h,w $，Joe 在 Michael 看不见的情况下盖住任意一个 $ h \times w $ 的子矩阵，然后问 Michael 这个子矩阵中最大的数是多少。Michael 答对即为获胜。现在，要对每一次给出的矩阵找出一对最小的 $ h,w $，使得 Michael 一定能赢。

**输入格式**

第一行一个整数 $ t $，表示有 $ t $ 组数据。

接下来对于每一组数据：

第一行两个正整数 $ n, m $，表示一个 $ n \times m $ 的矩阵。

接下来 $ n $ 行，每行 $ m $ 个数，表示这个矩阵中的元素。

**输出格式**

对于每组数据，输出一个整数表示我们选出的 $ h,w $ 的乘积。

**输入输出样例**

**样例输入 #1**

```plaintext
3
1 1
3
4 4
2 12 6 10
3 15 16 4
1 13 8 11
14 7 9 5
2 3
-7 5 2
0 8 -3
```

**样例输出 #1**

```plaintext
1
9
4
```

**说明/提示**

在第一组数据中，矩阵是 $ 1 \times 1 $ 的，因此对于 $ h,w $，唯一可能的选择是 $ h=1, w=1 $，给出了 $ h \cdot w = 1 $ 的面积。

描述中展示了第二组数据给出的矩阵。可以证明，只要 $ h=3, w=3 $，Michael 就能保证胜利，而只要 $ h \cdot w \le 8 $，任何选择都不能保证胜利。

对于所有数据，$ 1 \le t \le 20, 1 \le n, m \le 40, -10^9 \le $ 矩阵中的元素 $ \le 10^9 $。

**题目描述**

Michael 和 Joe 在玩一个游戏。游戏在一个有 $ n $ 行 $ m $ 列的网格上进行，网格中填满了不同的整数。我们用 $ (i, j) $ 表示第 $ i $ 行（$ 1 \le i \le n $）和第 $ j $ 列（$ 1 \le j \le m $）的方格，以及该方格中的数字 $ a_{ij} $。

Michael 首先说出两个数字 $ h $（$ 1 \le h \le n $）和 $ w $（$ 1 \le w \le m $）。然后 Joe 可以选择网格中的任意 $ h \times w $ 子矩形（不让 Michael 看见）。

形式上，一个 $ h \times w $ 子矩形从某个方格 $ (a, b) $ 开始，其中 $ 1 \le a \le n-h+1 $ 和 $ 1 \le b \le m-w+1 $。它包含所有方格 $ (i, j) $ 对于 $ a \le i \le a+h-1 $ 和 $ b \le j \le b+w-1 $。

最后，Michael 必须猜测子矩形中的最大数。如果他猜对了，他就赢了。

因为 Michael 不喜欢大数字，他希望选择的子矩形的面积（即 $ h \cdot w $）尽可能小，同时仍然确保他能够赢，而不依赖于 Joe 的选择。帮助 Michael 找到这个最小可能的面积。

可以证明 Michael 总是可以选择 $ h, w $，使得他能够确保胜利。

**输入输出格式**

**输入格式**

每个测试包含多个测试用例。第一行包含测试用例的数量 $ t $（$ 1 \le t \le 20 $）。接下来是测试用例的描述。

每个测试用例的第一行包含两个整数 $ n $ 和 $ m $（$ 1 \le n, m \le 40 $）—— 网格的大小。

接下来的 $ n $ 行每行包含 $ m $ 个整数。第 $ i $ 行的第 $ j $ 个整数是 $ a_{ij} $（$ -10^9 \le a_{ij} \le 10^9 $）—— 单元格 $ (i, j) $ 中的元素。

保证所有数字都是不同的（即，如果 $ a_{i_1j_1} = a_{i_2j_2} $，那么 $ i_1 = i_2, j_1 = j_2 $）。

**输出格式**

对于每个测试用例，打印一个正整数——在仍然确保 Michael 能够保证胜利的情况下，子矩形可以具有的最小可能面积。**题意翻译** Michael 和 Joe 在玩一个游戏。一共有 $ t $ 次，每次 Michael 给出一个 $ n \times m $ 的矩阵和一对 $ h,w $，Joe 在 Michael 看不见的情况下盖住任意一个 $ h \times w $ 的子矩阵，然后问 Michael 这个子矩阵中最大的数是多少。Michael 答对即为获胜。现在，要对每一次给出的矩阵找出一对最小的 $ h,w $，使得 Michael 一定能赢。 **输入格式** 第一行一个整数 $ t $，表示有 $ t $ 组数据。 接下来对于每一组数据： 第一行两个正整数 $ n, m $，表示一个 $ n \times m $ 的矩阵。 接下来 $ n $ 行，每行 $ m $ 个数，表示这个矩阵中的元素。 **输出格式** 对于每组数据，输出一个整数表示我们选出的 $ h,w $ 的乘积。 **输入输出样例** **样例输入 #1** ```plaintext 3 1 1 3 4 4 2 12 6 10 3 15 16 4 1 13 8 11 14 7 9 5 2 3 -7 5 2 0 8 -3 ``` **样例输出 #1** ```plaintext 1 9 4 ``` **说明/提示** 在第一组数据中，矩阵是 $ 1 \times 1 $ 的，因此对于 $ h,w $，唯一可能的选择是 $ h=1, w=1 $，给出了 $ h \cdot w = 1 $ 的面积。 描述中展示了第二组数据给出的矩阵。可以证明，只要 $ h=3, w=3 $，Michael 就能保证胜利，而只要 $ h \cdot w \le 8 $，任何选择都不能保证胜利。 对于所有数据，$ 1 \le t \le 20, 1 \le n, m \le 40, -10^9 \le $ 矩阵中的元素 $ \le 10^9 $。 **题目描述** Michael 和 Joe 在玩一个游戏。游戏在一个有 $ n $ 行 $ m $ 列的网格上进行，网格中填满了不同的整数。我们用 $ (i, j) $ 表示第 $ i $ 行（$ 1 \le i \le n $）和第 $ j $ 列（$ 1 \le j \le m $）的方格，以及该方格中的数字 $ a_{ij} $。 Michael 首先说出两个数字 $ h $（$ 1 \le h \le n $）和 $ w $（$ 1 \le w \le m $）。然后 Joe 可以选择网格中的任意 $ h \times w $ 子矩形（不让 Michael 看见）。 形式上，一个 $ h \times w $ 子矩形从某个方格 $ (a, b) $ 开始，其中 $ 1 \le a \le n-h+1 $ 和 $ 1 \le b \le m-w+1 $。它包含所有方格 $ (i, j) $ 对于 $ a \le i \le a+h-1 $ 和 $ b \le j \le b+w-1 $。 最后，Michael 必须猜测子矩形中的最大数。如果他猜对了，他就赢了。 因为 Michael 不喜欢大数字，他希望选择的子矩形的面积（即 $ h \cdot w $）尽可能小，同时仍然确保他能够赢，而不依赖于 Joe 的选择。帮助 Michael 找到这个最小可能的面积。 可以证明 Michael 总是可以选择 $ h, w $，使得他能够确保胜利。 **输入输出格式** **输入格式** 每个测试包含多个测试用例。第一行包含测试用例的数量 $ t $（$ 1 \le t \le 20 $）。接下来是测试用例的描述。 每个测试用例的第一行包含两个整数 $ n $ 和 $ m $（$ 1 \le n, m \le 40 $）—— 网格的大小。 接下来的 $ n $ 行每行包含 $ m $ 个整数。第 $ i $ 行的第 $ j $ 个整数是 $ a_{ij} $（$ -10^9 \le a_{ij} \le 10^9 $）—— 单元格 $ (i, j) $ 中的元素。 保证所有数字都是不同的（即，如果 $ a_{i_1j_1} = a_{i_2j_2} $，那么 $ i_1 = i_2, j_1 = j_2 $）。 **输出格式** 对于每个测试用例，打印一个正整数——在仍然确保 Michael 能够保证胜利的情况下，子矩形可以具有的最小可能面积。