Circular Spanning Tree

题意翻译

有 $T$ 组数据，每组数据有一个长度为 $n$ 的 $\tt 01$ 字符串，求构造一个 $n$ 个结点的树满足每个结点的度数的奇偶性符合 $\tt 01$ 串 $s$，且将这些点依次排列到一个环上，任意两条边不在非端点处相交。

题目描述

There are $ n $ nodes arranged in a circle numbered from $ 1 $ to $ n $ in the clockwise order. You are also given a binary string $ s $ of length $ n $ . Your task is to construct a tree on the given $ n $ nodes satisfying the two conditions below or report that there such tree does not exist: - For each node $ i $ $ (1 \le i \le n) $ , the degree of node is even if $ s_i = 0 $ and odd if $ s_i = 1 $ . - No two edges of the tree intersect internally in the circle. The edges are allowed to intersect on the circumference. Note that all edges are drawn as straight line segments. For example, edge $ (u, v) $ in the tree is drawn as a line segment connecting $ u $ and $ v $ on the circle. A tree on $ n $ nodes is a connected graph with $ n - 1 $ edges.

输入输出格式

输入格式

The input consists of multiple test cases. The first line contains a single integer $ t $ $ (1 \leq t \leq 2\cdot 10^4) $ — the number of test cases. Description of the test cases follows. The first line of each test case contains a single integer $ n $ $ (2 \leq n \leq 2\cdot 10^5) $ — the number of nodes. The second line of each test case contains a binary string $ s $ of length $ n $ . It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2\cdot 10^5 $ .

输出格式

For each test case, if there does not exist a tree that satisfies the given conditions, then output "NO" (without quotes), otherwise output "YES" followed by the description of tree. You can output each letter in any case (for example, "YES", "Yes", "yes", "yEs", "yEs" will be recognized as a positive answer). If there exists a tree, then output $ n - 1 $ lines, each containing two integers $ u $ and $ v $ $ (1 \leq u,v \leq n, u \neq v) $ denoting an edge between $ u $ and $ v $ in the tree. If there are multiple possible answers, output any.

输入输出样例

输入样例 #1

3
4
0110
2
10
6
110110

输出样例 #1

YES
2 1
3 4
1 4
NO
YES
2 3
1 2
5 6
6 2
3 4

说明

In the first test case, the tree looks as follows: 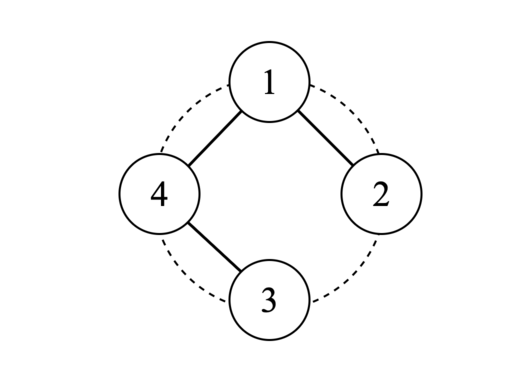In the second test case, there is only one possible tree with an edge between $ 1 $ and $ 2 $ , and it does not satisfy the degree constraints. In the third test case, 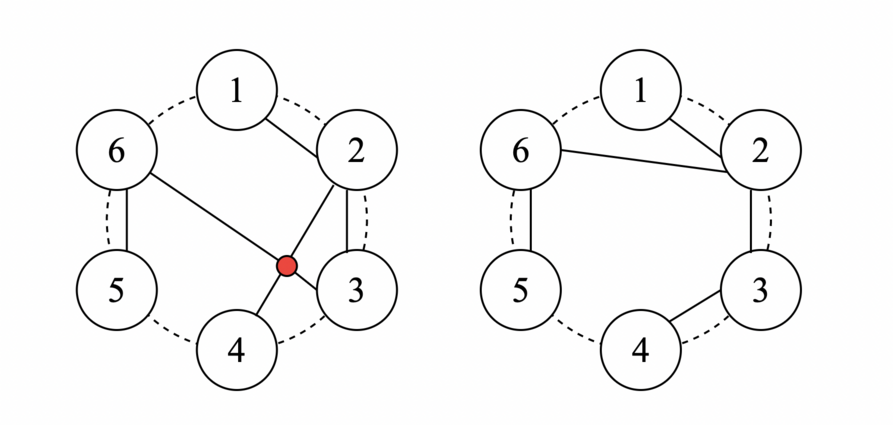 The tree on the left satisfies the degree constraints but the edges intersect internally, therefore it is not a valid tree, while the tree on the right is valid.

题目大意：
给定一个长度为 $ n $ 的01字符串 $ s $，构造一个 $ n $ 个节点的树，使得每个节点的度数与字符串 $ s $ 中的对应位相匹配（即 $ s_i = 0 $ 时度数为偶数，$ s_i = 1 $ 时度数为奇数），并且这些节点依次排列在一个环上，任意两条边不在非端点处相交。

输入输出数据格式：
输入包括多个测试用例。第一行包含一个整数 $ t $（$ 1 \leq t \leq 2 \times 10^4 $），表示测试用例的数量。接下来是每个测试用例的描述。

每个测试用例的第一行包含一个整数 $ n $（$ 2 \leq n \leq 2 \times 10^5 $），表示节点的数量。第二行包含一个长度为 $ n $ 的二进制字符串 $ s $。

对于每个测试用例，如果不存在满足给定条件的树，则输出 "NO"，否则输出 "YES" 并描述树的边。如果存在多棵可能的树，输出其中任意一棵。

每个测试用例的输出包含 $ n - 1 $ 行，每行包含两个整数 $ u $ 和 $ v $（$ 1 \leq u, v \leq n, u \neq v $），表示树中 $ u $ 和 $ v $ 之间的一条边。题目大意： 给定一个长度为 $ n $ 的01字符串 $ s $，构造一个 $ n $ 个节点的树，使得每个节点的度数与字符串 $ s $ 中的对应位相匹配（即 $ s_i = 0 $ 时度数为偶数，$ s_i = 1 $ 时度数为奇数），并且这些节点依次排列在一个环上，任意两条边不在非端点处相交。 输入输出数据格式： 输入包括多个测试用例。第一行包含一个整数 $ t $（$ 1 \leq t \leq 2 \times 10^4 $），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $ n $（$ 2 \leq n \leq 2 \times 10^5 $），表示节点的数量。第二行包含一个长度为 $ n $ 的二进制字符串 $ s $。 对于每个测试用例，如果不存在满足给定条件的树，则输出 "NO"，否则输出 "YES" 并描述树的边。如果存在多棵可能的树，输出其中任意一棵。 每个测试用例的输出包含 $ n - 1 $ 行，每行包含两个整数 $ u $ 和 $ v $（$ 1 \leq u, v \leq n, u \neq v $），表示树中 $ u $ 和 $ v $ 之间的一条边。