309451: CF1680F. Lenient Vertex Cover
Memory Limit:512 MB
Time Limit:5 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Lenient Vertex Cover
题意翻译
**本题有多测。** 定义一个点集是“宽松的”,当且仅当满足: - 每条边都有至少一个顶点在这个点集中 - 最多只能有一条边,满足两个顶点都在这个点集中 请你找出一个“宽松的”点集。 如果有,输出 `YES` 和一个字符串 $s$,$s_i=0$ 表示 $i$ 不在点集中,$s_i=1$ 表示 $i$ 在点集中。如果有多种合法方案,输出任意一个。 如果没有,输出 `NO`。题目描述
You are given a simple connected undirected graph, consisting of $ n $ vertices and $ m $ edges. The vertices are numbered from $ 1 $ to $ n $ . A vertex cover of a graph is a set of vertices such that each edge has at least one of its endpoints in the set. Let's call a lenient vertex cover such a vertex cover that at most one edge in it has both endpoints in the set. Find a lenient vertex cover of a graph or report that there is none. If there are multiple answers, then print any of them.输入输出格式
输入格式
The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of testcases. The first line of each testcase contains two integers $ n $ and $ m $ ( $ 2 \le n \le 10^6 $ ; $ n - 1 \le m \le \min(10^6, \frac{n \cdot (n - 1)}{2}) $ ) — the number of vertices and the number of edges of the graph. Each of the next $ m $ lines contains two integers $ v $ and $ u $ ( $ 1 \le v, u \le n $ ; $ v \neq u $ ) — the descriptions of the edges. For each testcase, the graph is connected and doesn't have multiple edges. The sum of $ n $ over all testcases doesn't exceed $ 10^6 $ . The sum of $ m $ over all testcases doesn't exceed $ 10^6 $ .
输出格式
For each testcase, the first line should contain YES if a lenient vertex cover exists, and NO otherwise. If it exists, the second line should contain a binary string $ s $ of length $ n $ , where $ s_i = 1 $ means that vertex $ i $ is in the vertex cover, and $ s_i = 0 $ means that vertex $ i $ isn't. If there are multiple answers, then print any of them.
输入输出样例
输入样例 #1
4
6 5
1 3
2 4
3 4
3 5
4 6
4 6
1 2
2 3
3 4
1 4
1 3
2 4
8 11
1 3
2 4
3 5
4 6
5 7
6 8
1 2
3 4
5 6
7 8
7 2
4 5
1 2
2 3
3 4
1 3
2 4输出样例 #1
YES
001100
NO
YES
01100110
YES
0110输入样例 #2
1
10 15
9 4
3 4
6 4
1 2
8 2
8 3
7 2
9 5
7 8
5 10
1 4
2 10
5 3
5 7
2 9输出样例 #2
YES
0101100100输入样例 #3
1
10 19
7 9
5 3
3 4
1 6
9 4
1 4
10 5
7 1
9 2
8 3
7 3
10 9
2 10
9 8
3 2
1 5
10 7
9 5
1 2输出样例 #3
YES
1010000011说明
Here are the graphs from the first example. The vertices in the lenient vertex covers are marked red. 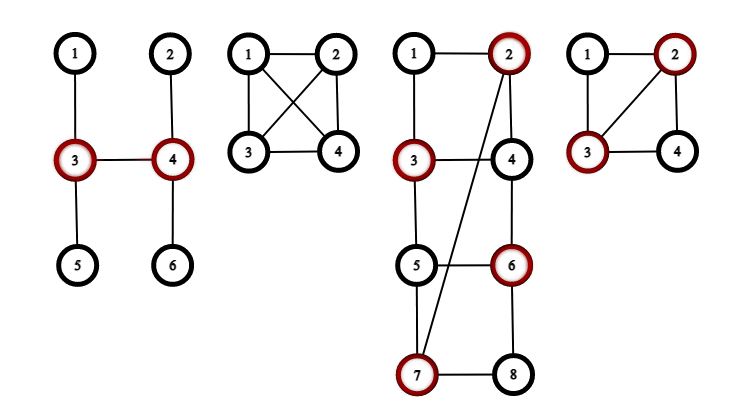Input
题意翻译
**本题有多测。** 定义一个点集是“宽松的”,当且仅当满足: - 每条边都有至少一个顶点在这个点集中 - 最多只能有一条边,满足两个顶点都在这个点集中 请你找出一个“宽松的”点集。 如果有,输出 `YES` 和一个字符串 $s$,$s_i=0$ 表示 $i$ 不在点集中,$s_i=1$ 表示 $i$ 在点集中。如果有多种合法方案,输出任意一个。 如果没有,输出 `NO`。Output
**宽松顶点覆盖**
**题意翻译**
**本题有多测。**
定义一个点集是“宽松的”,当且仅当满足:
- 每条边都有至少一个顶点在这个点集中
- 最多只能有一条边,满足两个顶点都在这个点集中
请你找出一个“宽松的”点集。
如果有,输出 `YES` 和一个字符串 \( s \),\( s_i=0 \) 表示 \( i \) 不在点集中,\( s_i=1 \) 表示 \( i \) 在点集中。如果有多种合法方案,输出任意一个。
如果没有,输出 `NO`。
**题目描述**
给定一个简单连通无向图,由 \( n \) 个顶点和 \( m \) 条边组成。顶点编号从 \( 1 \) 到 \( n \)。
图的一个顶点覆盖是一个顶点集合,使得每条边至少有一个端点在这个集合中。
我们将一个宽松顶点覆盖定义为这样一个顶点覆盖,其中最多只有一条边,它的两个端点都在集合中。
找出一个图的宽松顶点覆盖,或者报告说不存在。如果有多个答案,那么输出其中任何一个。
**输入输出格式**
**输入格式**
第一行包含一个整数 \( t \) (\( 1 \le t \le 10^4 \))——测试用例的数量。
每个测试用例的第一行包含两个整数 \( n \) 和 \( m \) (\( 2 \le n \le 10^6 \); \( n - 1 \le m \le \min(10^6, \frac{n \cdot (n - 1)}{2}) \))——图的顶点数和边数。
接下来的 \( m \) 行每行包含两个整数 \( v \) 和 \( u \) (\( 1 \le v, u \le n \); \( v \neq u \))——边的描述。
对于每个测试用例,图是连通的,并且没有多条边。所有测试用例的 \( n \) 之和不超过 \( 10^6 \)。所有测试用例的 \( m \) 之和不超过 \( 10^6 \)。
**输出格式**
对于每个测试用例,如果存在宽松顶点覆盖,第一行应包含 `YES`,否则包含 `NO`。如果存在,第二行应包含一个长度为 \( n \) 的二进制字符串 \( s \),其中 \( s_i = 1 \) 表示顶点 \( i \) 在顶点覆盖中,\( s_i = 0 \) 表示顶点 \( i \) 不在。
如果有多个答案,那么输出其中任何一个。
**输入输出样例**
**输入样例 #1**
```
4
6 5
1 3
2 4
3 4
3 5
4 6
4 6
1 2
2 3
3 4
1 4
1 3
2 4
8 11
1 3
2 4
3 5
4 6
5 7
6 8
1 2
3 4
5 6
7 8
7 2
4 5
1 2
2 3
3 4
1 3
2 4
```
**输出样例 #1**
```
YES
001100
NO
YES
01100110
YES
0110
```
**输入样例 #2**
```
1
10 15
9 4
3 4
6 4
1 2
8 2
8 3
7 2
9 5
7 8
5 10
1 4
2 10
5 3
5 7
2 9
```
**输出样例 #2**
```
YES
0101100100
```
**输入样例 #3**
```
1
10 19
7 9
5 3
3 4
1 6
9 4
1 4
10 5
7 1
9 2
8 3
7 3
10 9
2 10
9 8
3 2
1 5
10 7
9 5
1 2
```
**输出样例 #3**
```
YES
1010000011
```
**说明**
这里是从第一个示例中的图。宽松顶点覆盖中的顶点标记为红色。
**宽松顶点覆盖** **题意翻译** **本题有多测。** 定义一个点集是“宽松的”,当且仅当满足: - 每条边都有至少一个顶点在这个点集中 - 最多只能有一条边,满足两个顶点都在这个点集中 请你找出一个“宽松的”点集。 如果有,输出 `YES` 和一个字符串 \( s \),\( s_i=0 \) 表示 \( i \) 不在点集中,\( s_i=1 \) 表示 \( i \) 在点集中。如果有多种合法方案,输出任意一个。 如果没有,输出 `NO`。 **题目描述** 给定一个简单连通无向图,由 \( n \) 个顶点和 \( m \) 条边组成。顶点编号从 \( 1 \) 到 \( n \)。 图的一个顶点覆盖是一个顶点集合,使得每条边至少有一个端点在这个集合中。 我们将一个宽松顶点覆盖定义为这样一个顶点覆盖,其中最多只有一条边,它的两个端点都在集合中。 找出一个图的宽松顶点覆盖,或者报告说不存在。如果有多个答案,那么输出其中任何一个。 **输入输出格式** **输入格式** 第一行包含一个整数 \( t \) (\( 1 \le t \le 10^4 \))——测试用例的数量。 每个测试用例的第一行包含两个整数 \( n \) 和 \( m \) (\( 2 \le n \le 10^6 \); \( n - 1 \le m \le \min(10^6, \frac{n \cdot (n - 1)}{2}) \))——图的顶点数和边数。 接下来的 \( m \) 行每行包含两个整数 \( v \) 和 \( u \) (\( 1 \le v, u \le n \); \( v \neq u \))——边的描述。 对于每个测试用例,图是连通的,并且没有多条边。所有测试用例的 \( n \) 之和不超过 \( 10^6 \)。所有测试用例的 \( m \) 之和不超过 \( 10^6 \)。 **输出格式** 对于每个测试用例,如果存在宽松顶点覆盖,第一行应包含 `YES`,否则包含 `NO`。如果存在,第二行应包含一个长度为 \( n \) 的二进制字符串 \( s \),其中 \( s_i = 1 \) 表示顶点 \( i \) 在顶点覆盖中,\( s_i = 0 \) 表示顶点 \( i \) 不在。 如果有多个答案,那么输出其中任何一个。 **输入输出样例** **输入样例 #1** ``` 4 6 5 1 3 2 4 3 4 3 5 4 6 4 6 1 2 2 3 3 4 1 4 1 3 2 4 8 11 1 3 2 4 3 5 4 6 5 7 6 8 1 2 3 4 5 6 7 8 7 2 4 5 1 2 2 3 3 4 1 3 2 4 ``` **输出样例 #1** ``` YES 001100 NO YES 01100110 YES 0110 ``` **输入样例 #2** ``` 1 10 15 9 4 3 4 6 4 1 2 8 2 8 3 7 2 9 5 7 8 5 10 1 4 2 10 5 3 5 7 2 9 ``` **输出样例 #2** ``` YES 0101100100 ``` **输入样例 #3** ``` 1 10 19 7 9 5 3 3 4 1 6 9 4 1 4 10 5 7 1 9 2 8 3 7 3 10 9 2 10 9 8 3 2 1 5 10 7 9 5 1 2 ``` **输出样例 #3** ``` YES 1010000011 ``` **说明** 这里是从第一个示例中的图。宽松顶点覆盖中的顶点标记为红色。 
**题意翻译**
**本题有多测。**
定义一个点集是“宽松的”,当且仅当满足:
- 每条边都有至少一个顶点在这个点集中
- 最多只能有一条边,满足两个顶点都在这个点集中
请你找出一个“宽松的”点集。
如果有,输出 `YES` 和一个字符串 \( s \),\( s_i=0 \) 表示 \( i \) 不在点集中,\( s_i=1 \) 表示 \( i \) 在点集中。如果有多种合法方案,输出任意一个。
如果没有,输出 `NO`。
**题目描述**
给定一个简单连通无向图,由 \( n \) 个顶点和 \( m \) 条边组成。顶点编号从 \( 1 \) 到 \( n \)。
图的一个顶点覆盖是一个顶点集合,使得每条边至少有一个端点在这个集合中。
我们将一个宽松顶点覆盖定义为这样一个顶点覆盖,其中最多只有一条边,它的两个端点都在集合中。
找出一个图的宽松顶点覆盖,或者报告说不存在。如果有多个答案,那么输出其中任何一个。
**输入输出格式**
**输入格式**
第一行包含一个整数 \( t \) (\( 1 \le t \le 10^4 \))——测试用例的数量。
每个测试用例的第一行包含两个整数 \( n \) 和 \( m \) (\( 2 \le n \le 10^6 \); \( n - 1 \le m \le \min(10^6, \frac{n \cdot (n - 1)}{2}) \))——图的顶点数和边数。
接下来的 \( m \) 行每行包含两个整数 \( v \) 和 \( u \) (\( 1 \le v, u \le n \); \( v \neq u \))——边的描述。
对于每个测试用例,图是连通的,并且没有多条边。所有测试用例的 \( n \) 之和不超过 \( 10^6 \)。所有测试用例的 \( m \) 之和不超过 \( 10^6 \)。
**输出格式**
对于每个测试用例,如果存在宽松顶点覆盖,第一行应包含 `YES`,否则包含 `NO`。如果存在,第二行应包含一个长度为 \( n \) 的二进制字符串 \( s \),其中 \( s_i = 1 \) 表示顶点 \( i \) 在顶点覆盖中,\( s_i = 0 \) 表示顶点 \( i \) 不在。
如果有多个答案,那么输出其中任何一个。
**输入输出样例**
**输入样例 #1**
```
4
6 5
1 3
2 4
3 4
3 5
4 6
4 6
1 2
2 3
3 4
1 4
1 3
2 4
8 11
1 3
2 4
3 5
4 6
5 7
6 8
1 2
3 4
5 6
7 8
7 2
4 5
1 2
2 3
3 4
1 3
2 4
```
**输出样例 #1**
```
YES
001100
NO
YES
01100110
YES
0110
```
**输入样例 #2**
```
1
10 15
9 4
3 4
6 4
1 2
8 2
8 3
7 2
9 5
7 8
5 10
1 4
2 10
5 3
5 7
2 9
```
**输出样例 #2**
```
YES
0101100100
```
**输入样例 #3**
```
1
10 19
7 9
5 3
3 4
1 6
9 4
1 4
10 5
7 1
9 2
8 3
7 3
10 9
2 10
9 8
3 2
1 5
10 7
9 5
1 2
```
**输出样例 #3**
```
YES
1010000011
```
**说明**
这里是从第一个示例中的图。宽松顶点覆盖中的顶点标记为红色。
**宽松顶点覆盖** **题意翻译** **本题有多测。** 定义一个点集是“宽松的”,当且仅当满足: - 每条边都有至少一个顶点在这个点集中 - 最多只能有一条边,满足两个顶点都在这个点集中 请你找出一个“宽松的”点集。 如果有,输出 `YES` 和一个字符串 \( s \),\( s_i=0 \) 表示 \( i \) 不在点集中,\( s_i=1 \) 表示 \( i \) 在点集中。如果有多种合法方案,输出任意一个。 如果没有,输出 `NO`。 **题目描述** 给定一个简单连通无向图,由 \( n \) 个顶点和 \( m \) 条边组成。顶点编号从 \( 1 \) 到 \( n \)。 图的一个顶点覆盖是一个顶点集合,使得每条边至少有一个端点在这个集合中。 我们将一个宽松顶点覆盖定义为这样一个顶点覆盖,其中最多只有一条边,它的两个端点都在集合中。 找出一个图的宽松顶点覆盖,或者报告说不存在。如果有多个答案,那么输出其中任何一个。 **输入输出格式** **输入格式** 第一行包含一个整数 \( t \) (\( 1 \le t \le 10^4 \))——测试用例的数量。 每个测试用例的第一行包含两个整数 \( n \) 和 \( m \) (\( 2 \le n \le 10^6 \); \( n - 1 \le m \le \min(10^6, \frac{n \cdot (n - 1)}{2}) \))——图的顶点数和边数。 接下来的 \( m \) 行每行包含两个整数 \( v \) 和 \( u \) (\( 1 \le v, u \le n \); \( v \neq u \))——边的描述。 对于每个测试用例,图是连通的,并且没有多条边。所有测试用例的 \( n \) 之和不超过 \( 10^6 \)。所有测试用例的 \( m \) 之和不超过 \( 10^6 \)。 **输出格式** 对于每个测试用例,如果存在宽松顶点覆盖,第一行应包含 `YES`,否则包含 `NO`。如果存在,第二行应包含一个长度为 \( n \) 的二进制字符串 \( s \),其中 \( s_i = 1 \) 表示顶点 \( i \) 在顶点覆盖中,\( s_i = 0 \) 表示顶点 \( i \) 不在。 如果有多个答案,那么输出其中任何一个。 **输入输出样例** **输入样例 #1** ``` 4 6 5 1 3 2 4 3 4 3 5 4 6 4 6 1 2 2 3 3 4 1 4 1 3 2 4 8 11 1 3 2 4 3 5 4 6 5 7 6 8 1 2 3 4 5 6 7 8 7 2 4 5 1 2 2 3 3 4 1 3 2 4 ``` **输出样例 #1** ``` YES 001100 NO YES 01100110 YES 0110 ``` **输入样例 #2** ``` 1 10 15 9 4 3 4 6 4 1 2 8 2 8 3 7 2 9 5 7 8 5 10 1 4 2 10 5 3 5 7 2 9 ``` **输出样例 #2** ``` YES 0101100100 ``` **输入样例 #3** ``` 1 10 19 7 9 5 3 3 4 1 6 9 4 1 4 10 5 7 1 9 2 8 3 7 3 10 9 2 10 9 8 3 2 1 5 10 7 9 5 1 2 ``` **输出样例 #3** ``` YES 1010000011 ``` **说明** 这里是从第一个示例中的图。宽松顶点覆盖中的顶点标记为红色。 