Cyclic Components

题意翻译

## 题目描述 给定一张 $n$ 个点，$m$ 条边的无向图。保证无重边、无自环。在该图的所有连通块中，你需要找出环的个数。 无向图的环的定义如下： 原无向图中的一个子图被定义为环，当且仅当它的点集重新排序后可以满足如下条件： - 第一个点与第二个点通过一条边相连接； - 第二个点与第三个点通过一条边相连接； - …… - 最后一个点与第一个点通过一条边相连接。 - 所有的边都应当是不同的。 - 其边集不应当包含除了以上所述的边以外的任何边。 这样，我们就称这个子图（点 + 边）为环。 根据定义，一个环至少需要包含三个点，且边数与点数应当是相同的。 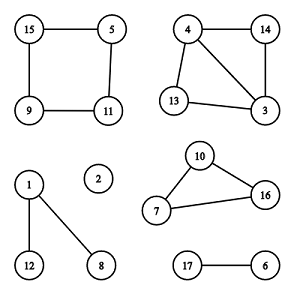 例如对于上图，共有 $6$ 个联通块，但只有 $[7,10,16]$ 和 $[5,11,9,15]$ 这两个联通块是环。 ## 输入输出格式 **输入格式：** 第一行两个整数 $n$ 和 $m$ $(1 \le n \le 2 \cdot 10^5, 0 \le m \le 2 \cdot 10^5)$，分别表示图的点数和无向边数。 接下来 $m$ 行，第 $i$ 行包含两个整数 $v_i, u_i$ $(1 \le v_i, u_i \le n, u_i \not = v_i)$，表示第 $i$ 条边连接着 $v_i$ 与 $u_i$ 两点。 **输出格式：** 输出一行一个整数，表示环的个数。 ## 说明 在第一个样例中，只有 $[3, 4, 5]$ 这个联通块是一个环。 第二个样例就对应着题目解释中的图片。

题目描述

You are given an undirected graph consisting of $ n $ vertices and $ m $ edges. Your task is to find the number of connected components which are cycles. Here are some definitions of graph theory. An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex $ a $ is connected with a vertex $ b $ , a vertex $ b $ is also connected with a vertex $ a $ ). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices. Two vertices $ u $ and $ v $ belong to the same connected component if and only if there is at least one path along edges connecting $ u $ and $ v $ . A connected component is a cycle if and only if its vertices can be reordered in such a way that: - the first vertex is connected with the second vertex by an edge, - the second vertex is connected with the third vertex by an edge, - ... - the last vertex is connected with the first vertex by an edge, - all the described edges of a cycle are distinct. A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices. 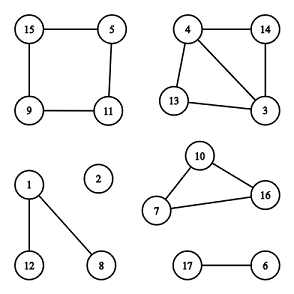There are $ 6 $ connected components, $ 2 $ of them are cycles: $ [7, 10, 16] $ and $ [5, 11, 9, 15] $ .

输入输出格式

输入格式

The first line contains two integer numbers $ n $ and $ m $ ( $ 1 \le n \le 2 \cdot 10^5 $ , $ 0 \le m \le 2 \cdot 10^5 $ ) — number of vertices and edges. The following $ m $ lines contains edges: edge $ i $ is given as a pair of vertices $ v_i $ , $ u_i $ ( $ 1 \le v_i, u_i \le n $ , $ u_i \ne v_i $ ). There is no multiple edges in the given graph, i.e. for each pair ( $ v_i, u_i $ ) there no other pairs ( $ v_i, u_i $ ) and ( $ u_i, v_i $ ) in the list of edges.

输出格式

Print one integer — the number of connected components which are also cycles.

输入输出样例

输入样例 #1

5 4
1 2
3 4
5 4
3 5

输出样例 #1

1

输入样例 #2

17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6

输出样例 #2

2

说明

In the first example only component $ [3, 4, 5] $ is also a cycle. The illustration above corresponds to the second example.

题意翻译

## 题目描述 给定一张 $n$ 个点，$m$ 条边的无向图。保证无重边、无自环。在该图的所有连通块中，你需要找出环的个数。 无向图的环的定义如下： 原无向图中的一个子图被定义为环，当且仅当它的点集重新排序后可以满足如下条件： - 第一个点与第二个点通过一条边相连接； - 第二个点与第三个点通过一条边相连接； - …… - 最后一个点与第一个点通过一条边相连接。 - 所有的边都应当是不同的。 - 其边集不应当包含除了以上所述的边以外的任何边。 这样，我们就称这个子图（点 + 边）为环。 根据定义，一个环至少需要包含三个点，且边数与点数应当是相同的。  例如对于上图，共有 $6$ 个联通块，但只有 $[7,10,16]$ 和 $[5,11,9,15]$ 这两个联通块是环。 ## 输入输出格式 **输入格式：** 第一行两个整数 $n$ 和 $m$ $(1 \le n \le 2 \cdot 10^5, 0 \le m \le 2 \cdot 10^5)$，分别表示图的点数和无向边数。 接下来 $m$ 行，第 $i$ 行包含两个整数 $v_i, u_i$ $(1 \le v_i, u_i \le n, u_i \not = v_i)$，表示第 $i$ 条边连接着 $v_i$ 与 $u_i$ 两点。 **输出格式：** 输出一行一个整数，表示环的个数。 ## 说明 在第一个样例中，只有 $[3, 4, 5]$ 这个联通块是一个环。 第二个样例就对应着题目解释中的图片。