Code For 1

题意翻译

- 有一个序列，初始时只有一个数 $n(0\le n\le2^{50})$。 - 对于序列中每一个 $>1$ 的数，拆分成三个数 $\lfloor\frac n2\rfloor,n\bmod2,\lfloor\frac n2\rfloor$ 并替换原数，直到序列中没有>1的数为止。 - 查询最终序列中 $[l,r] (1\le l,r)$ 中有多少 $1$。 - 同时 $l,r$ 满足 $0\le r - l\le10^5$。

题目描述

Jon fought bravely to rescue the wildlings who were attacked by the white-walkers at Hardhome. On his arrival, Sam tells him that he wants to go to Oldtown to train at the Citadel to become a maester, so he can return and take the deceased Aemon's place as maester of Castle Black. Jon agrees to Sam's proposal and Sam sets off his journey to the Citadel. However becoming a trainee at the Citadel is not a cakewalk and hence the maesters at the Citadel gave Sam a problem to test his eligibility. Initially Sam has a list with a single element $ n $ . Then he has to perform certain operations on this list. In each operation Sam must remove any element $ x $ , such that $ x>1 $ , from the list and insert at the same position 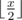, 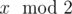, 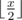 sequentially. He must continue with these operations until all the elements in the list are either $ 0 $ or $ 1 $ . Now the masters want the total number of $ 1 $ s in the range $ l $ to $ r $ ( $ 1 $ -indexed). Sam wants to become a maester but unfortunately he cannot solve this problem. Can you help Sam to pass the eligibility test?

输入输出格式

输入格式

The first line contains three integers $ n $ , $ l $ , $ r $ ( $ 0<=n&lt;2^{50} $ , $ 0<=r-l<=10^{5} $ , $ r>=1 $ , $ l>=1 $ ) – initial element and the range $ l $ to $ r $ . It is guaranteed that $ r $ is not greater than the length of the final list.

输出格式

Output the total number of $ 1 $ s in the range $ l $ to $ r $ in the final sequence.

输入输出样例

输入样例 #1

7 2 5

输出样例 #1

4

输入样例 #2

10 3 10

输出样例 #2

5

说明

Consider first example:  Elements on positions from $ 2 $ -nd to $ 5 $ -th in list is $ [1,1,1,1] $ . The number of ones is $ 4 $ . For the second example:  Elements on positions from $ 3 $ -rd to $ 10 $ -th in list is $ [1,1,1,0,1,0,1,0] $ . The number of ones is $ 5 $ .

题意翻译

- 有一个序列，初始时只有一个数 $n(0\le n\le2^{50})$。 - 对于序列中每一个 $>1$ 的数，拆分成三个数 $\lfloor\frac n2\rfloor,n\bmod2,\lfloor\frac n2\rfloor$ 并替换原数，直到序列中没有>1的数为止。 - 查询最终序列中 $[l,r] (1\le l,r)$ 中有多少 $1$。 - 同时 $l,r$ 满足 $0\le r - l\le10^5$。