Bearish Fanpages

题意翻译

给定一个 $n$ 个点的基环内向树森林，即给定每个点 $i$ 的后继 $f_i$。 （**特别地，保证在任意时刻，这个基环内向森林中的环长都** $\boldsymbol{\ge 3}$） 在这个限制下，考虑与某个点 $i$ 距离不超过 $1$ 的点，也就是 $i$ 本身，$i$ 的后继 $f_i$ 以及若干个后继为 $i$ 的点。 不妨假设有 $k$ 个点的后继为 $i$，则我们需要考虑这 $k + 2$ 个点（这是因为环长 $\ge 3$，不会出现重复的点）。 称这 $k + 2$ 个点分别为 $i, j_0, j_1, j_2, \ldots , j_k$（$j_0$ 为 $i$ 的后继，$j_{1 \ldots k}$ 为后继为 $i$ 的那 $k$ 个点）。 现在假设**神秘事件**发生了，每个点都会进入一些人，第 $i$ 个点会进入 $t_i$ 个人。 恰好 $\left\lfloor \frac{t_i}{k+2} \right\rfloor$ 个人会进入 $j_0, j_1, j_2, \ldots , j_k$ 号点（每个点都进入 $\left\lfloor \frac{t_i}{k+2} \right\rfloor$ 个人），剩下的 $t_i - (k + 1) \cdot \!\left\lfloor \frac{t_i}{k+2} \right\rfloor$ 个人会留在点 $i$。 你需要依次处理 $q$ 个操作： 1. `1 i j`：将 $f_i$ 改为 $j$，即把 $i$ 的后继变成 $j$。保证仍然满足上文中的条件。 2. `2 i`：计算当**神秘事件**发生时，第 $i$ 个点最终会留下多少人。 3. `3`：计算当**神秘事件**发生时，每个点内最终留下的人数的最小值和最大值。 注意：每次**神秘事件**发生都是互不影响的。

题目描述

There is a social website with $ n $ fanpages, numbered $ 1 $ through $ n $ . There are also $ n $ companies, and the $ i $ -th company owns the $ i $ -th fanpage. Recently, the website created a feature called following. Each fanpage must choose exactly one other fanpage to follow. The website doesn’t allow a situation where $ i $ follows $ j $ and at the same time $ j $ follows $ i $ . Also, a fanpage can't follow itself. Let’s say that fanpage $ i $ follows some other fanpage $ j_{0} $ . Also, let’s say that $ i $ is followed by $ k $ other fanpages $ j_{1},j_{2},...,j_{k} $ . Then, when people visit fanpage $ i $ they see ads from $ k+2 $ distinct companies: $ i,j_{0},j_{1},...,j_{k} $ . Exactly $ t_{i} $ people subscribe (like) the $ i $ -th fanpage, and each of them will click exactly one add. For each of $ k+1 $ companies $ j_{0},j_{1},...,j_{k} $ , exactly 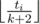 people will click their ad. Remaining 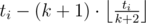 people will click an ad from company $ i $ (the owner of the fanpage). The total income of the company is equal to the number of people who click ads from this copmany. Limak and Radewoosh ask you for help. Initially, fanpage $ i $ follows fanpage $ f_{i} $ . Your task is to handle $ q $ queries of three types: - 1 i j — fanpage $ i $ follows fanpage $ j $ from now. It's guaranteed that $ i $ didn't follow $ j $ just before the query. Note an extra constraint for the number of queries of this type (below, in the Input section). - 2 i — print the total income of the $ i $ -th company. - 3 — print two integers: the smallest income of one company and the biggest income of one company.

输入输出格式

输入格式

The first line of the input contains two integers $ n $ and $ q $ ( $ 3<=n<=100000 $ , $ 1<=q<=100000 $ ) — the number of fanpages and the number of queries, respectively. The second line contains $ n $ integers $ t_{1},t_{2},...,t_{n} $ ( $ 1<=t_{i}<=10^{12} $ ) where $ t_{i} $ denotes the number of people subscribing the $ i $ -th fanpage. The third line contains $ n $ integers $ f_{1},f_{2},...,f_{n} $ ( $ 1<=f_{i}<=n $ ). Initially, fanpage $ i $ follows fanpage $ f_{i} $ . Then, $ q $ lines follow. The $ i $ -th of them describes the $ i $ -th query. The first number in the line is an integer $ type_{i} $ ( $ 1<=type_{i}<=3 $ ) — the type of the query. There will be at most $ 50000 $ queries of the first type. There will be at least one query of the second or the third type (so, the output won't be empty). It's guaranteed that at each moment a fanpage doesn't follow itself, and that no two fanpages follow each other.

输出格式

For each query of the second type print one integer in a separate line - the total income of the given company. For each query of the third type print two integers in a separate line - the minimum and the maximum total income, respectively.

输入输出样例

输入样例 #1

5 12
10 20 30 40 50
2 3 4 5 2
2 1
2 2
2 3
2 4
2 5
1 4 2
2 1
2 2
2 3
2 4
2 5
3

输出样例 #1

10
36
28
40
36
9
57
27
28
29
9 57

说明

In the sample test, there are $ 5 $ fanpages. The $ i $ -th of them has $ i·10 $ subscribers. On drawings, numbers of subscribers are written in circles. An arrow from $ A $ to $ B $ means that $ A $ follows $ B $ . The left drawing shows the initial situation. The first company gets income  from its own fanpage, and gets income  from the $ 2 $ -nd fanpage. So, the total income is $ 5+5=10 $ . After the first query ("2 1") you should print $ 10 $ . The right drawing shows the situation after a query "1 4 2" (after which fanpage $ 4 $ follows fanpage $ 2 $ ). Then, the first company still gets income $ 5 $ from its own fanpage, but now it gets only  from the $ 2 $ -nd fanpage. So, the total income is $ 5+4=9 $ now.