Levels and Regions

题意翻译

有一种电子游戏，它由$n$个关卡组成，每个关卡都被赋予了一个值$t_i$。 现在，你要将这些关卡分成$k$个级别，每个级别$j$对应了一段**连续的**关卡$[l_j,r_j]$，且必有$l_j\leq r_j$。任何一个关卡在且仅在一个级别中。 然后，一名玩家将会从第$1$个关卡，按顺序一直刷到第$n$个关卡。当他打到第$i$个关卡时，设这个关卡所在的级别是$j$，则他有 $\dfrac{t_i}{\sum\limits_{x=l_j}^{i}t_x}$ 的概率在$1$小时内AC这个关卡，然后进入下一关；或者没有AC这个关卡（但仍然花了$1$小时），还得再次挑战这个关卡。 你需要找到一种划分方法，使得该玩家期望AK该游戏的期望时间最小。输出这个最小的期望时间。

题目描述

Radewoosh is playing a computer game. There are $ n $ levels, numbered $ 1 $ through $ n $ . Levels are divided into $ k $ regions (groups). Each region contains some positive number of consecutive levels. The game repeats the the following process: 1. If all regions are beaten then the game ends immediately. Otherwise, the system finds the first region with at least one non-beaten level. Let $ X $ denote this region. 2. The system creates an empty bag for tokens. Each token will represent one level and there may be many tokens representing the same level. - For each already beaten level $ i $ in the region $ X $ , the system adds $ t_{i} $ tokens to the bag (tokens representing the $ i $ -th level). - Let $ j $ denote the first non-beaten level in the region $ X $ . The system adds $ t_{j} $ tokens to the bag. 3. Finally, the system takes a uniformly random token from the bag and a player starts the level represented by the token. A player spends one hour and beats the level, even if he has already beaten it in the past. Given $ n $ , $ k $ and values $ t_{1},t_{2},...,t_{n} $ , your task is to split levels into regions. Each level must belong to exactly one region, and each region must contain non-empty consecutive set of levels. What is the minimum possible expected number of hours required to finish the game?

输入输出格式

输入格式

The first line of the input contains two integers $ n $ and $ k $ ( $ 1<=n<=200000 $ , $ 1<=k<=min(50,n) $ ) — the number of levels and the number of regions, respectively. The second line contains $ n $ integers $ t_{1},t_{2},...,t_{n} $ ( $ 1<=t_{i}<=100000 $ ).

输出格式

Print one real number — the minimum possible expected value of the number of hours spent to finish the game if levels are distributed between regions in the optimal way. Your answer will be considered correct if its absolute or relative error does not exceed $ 10^{-4} $ . Namely: let's assume that your answer is $ a $ , and the answer of the jury is $ b $ . The checker program will consider your answer correct if .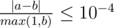

输入输出样例

输入样例 #1

4 2
100 3 5 7

输出样例 #1

5.7428571429

输入样例 #2

6 2
1 2 4 8 16 32

输出样例 #2

8.5000000000

说明

In the first sample, we are supposed to split $ 4 $ levels into $ 2 $ regions. It's optimal to create the first region with only one level (it must be the first level). Then, the second region must contain other three levels. In the second sample, it's optimal to split levels into two regions with $ 3 $ levels each.