Moodular Arithmetic

题意翻译

已知：$f(k*x \mod p)==k*f(x) \mod p$ 对于一个从f{0,1,2...p-1}→{0,1,2...p-1}的映射，问 对于给定的p和k，有多少种满足已知等式的映射 答案对$10^9+7$取模。

题目描述

As behooves any intelligent schoolboy, Kevin Sun is studying psycowlogy, cowculus, and cryptcowgraphy at the Bovinia State University (BGU) under Farmer Ivan. During his Mathematics of Olympiads (MoO) class, Kevin was confronted with a weird functional equation and needs your help. For two fixed integers $ k $ and $ p $ , where $ p $ is an odd prime number, the functional equation states that 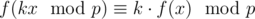for some function . (This equation should hold for any integer $ x $ in the range $ 0 $ to $ p-1 $ , inclusive.) It turns out that $ f $ can actually be many different functions. Instead of finding a solution, Kevin wants you to count the number of distinct functions $ f $ that satisfy this equation. Since the answer may be very large, you should print your result modulo $ 10^{9}+7 $ .

输入输出格式

输入格式

The input consists of two space-separated integers $ p $ and $ k $ ( $ 3<=p<=1000000 $ , $ 0<=k<=p-1 $ ) on a single line. It is guaranteed that $ p $ is an odd prime number.

输出格式

Print a single integer, the number of distinct functions $ f $ modulo $ 10^{9}+7 $ .

输入输出样例

输入样例 #1

3 2

输出样例 #1

3

输入样例 #2

5 4

输出样例 #2

25

说明

In the first sample, $ p=3 $ and $ k=2 $ . The following functions work: 1. $ f(0)=0 $ , $ f(1)=1 $ , $ f(2)=2 $ . 2. $ f(0)=0 $ , $ f(1)=2 $ , $ f(2)=1 $ . 3. $ f(0)=f(1)=f(2)=0 $ .