Acyclic Organic Compounds

题意翻译

+ 给定一棵有 $n$ 个节点的有根树 $T$，每个节点从 $1$ 到 $n$ 被编号，根为 $1$，每个节点都有一个字符。 对于一个节点 $v$ 的子树，从 $v$ 到子树中某一个节点的路径上的字符可以组成一个字符串（可能只有一个字符），定义所有不同的字符串的个数为 $\operatorname{dif}(v)$。 并且，对于每个节点 $v$ 都有一个数值 $c_v$，求 $\operatorname{dif}(v)+c_v$ 的最大值，以及最大值的个数。 + 第一行一个数 $n$ （$1\leq n\leq 3\times10^5$），表示树中节点的个数。 第二行 $n$ 个空格分隔的数 $c_i$ （$0\leq c_i\leq 10^9$）。 第三行一个小写英文字符组成的字符串，第 $i$ 个字符表示树上编号为 $i$ 的节点的字符。 接下来 $n-1$ 行描述了树的边。每一行给出两个用空格分隔的整数表示一条树边。 数据保证给出的是一棵树。 + 输出两行，第一行输出 $\operatorname{dif}(i)+c_i$ 的最大值，第二行输出最大值的个数。 + $1\leq n\leq 3\times10^5$，$0\leq c_i\leq 10^9$

题目描述

You are given a tree $ T $ with $ n $ vertices (numbered $ 1 $ through $ n $ ) and a letter in each vertex. The tree is rooted at vertex $ 1 $ . Let's look at the subtree $ T_{v} $ of some vertex $ v $ . It is possible to read a string along each simple path starting at $ v $ and ending at some vertex in $ T_{v} $ (possibly $ v $ itself). Let's denote the number of distinct strings which can be read this way as 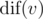. Also, there's a number $ c_{v} $ assigned to each vertex $ v $ . We are interested in vertices with the maximum value of 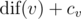. You should compute two statistics: the maximum value of 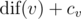 and the number of vertices $ v $ with the maximum .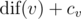

输入输出格式

输入格式

The first line of the input contains one integer $ n $ ( $ 1<=n<=300000 $ ) — the number of vertices of the tree. The second line contains $ n $ space-separated integers $ c_{i} $ ( $ 0<=c_{i}<=10^{9} $ ). The third line contains a string $ s $ consisting of $ n $ lowercase English letters — the $ i $ -th character of this string is the letter in vertex $ i $ . The following $ n-1 $ lines describe the tree $ T $ . Each of them contains two space-separated integers $ u $ and $ v $ ( $ 1<=u,v<=n $ ) indicating an edge between vertices $ u $ and $ v $ . It's guaranteed that the input will describe a tree.

输出格式

Print two lines. On the first line, print 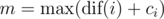 over all $ 1<=i<=n $ . On the second line, print the number of vertices $ v $ for which .

输入输出样例

输入样例 #1

10
1 2 7 20 20 30 40 50 50 50
cacabbcddd
1 2
6 8
7 2
6 2
5 4
5 9
3 10
2 5
2 3

输出样例 #1

51
3

输入样例 #2

6
0 2 4 1 1 1
raaaba
1 2
2 3
2 4
2 5
3 6

输出样例 #2

6
2

说明

In the first sample, the tree looks like this: The sets of strings that can be read from individual vertices are: Finally, the values of  are: In the second sample, the values of  are $ (5,4,2,1,1,1) $ . The distinct strings read in $ T_{2} $ are ; note that  can be read down to vertices $ 3 $ or $ 4 $ .