2240: NOIP2015:斗地主
Description
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中,牌的大小关系根据牌的数码表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色并不对牌的大小产生影响。每一局游戏中,一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌,首先打光自己的手牌一方取得游戏的胜利。
现在,牛牛只想知道,对于自己的若干组手牌,分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。
需要注意的是,本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。
具体规则如下:
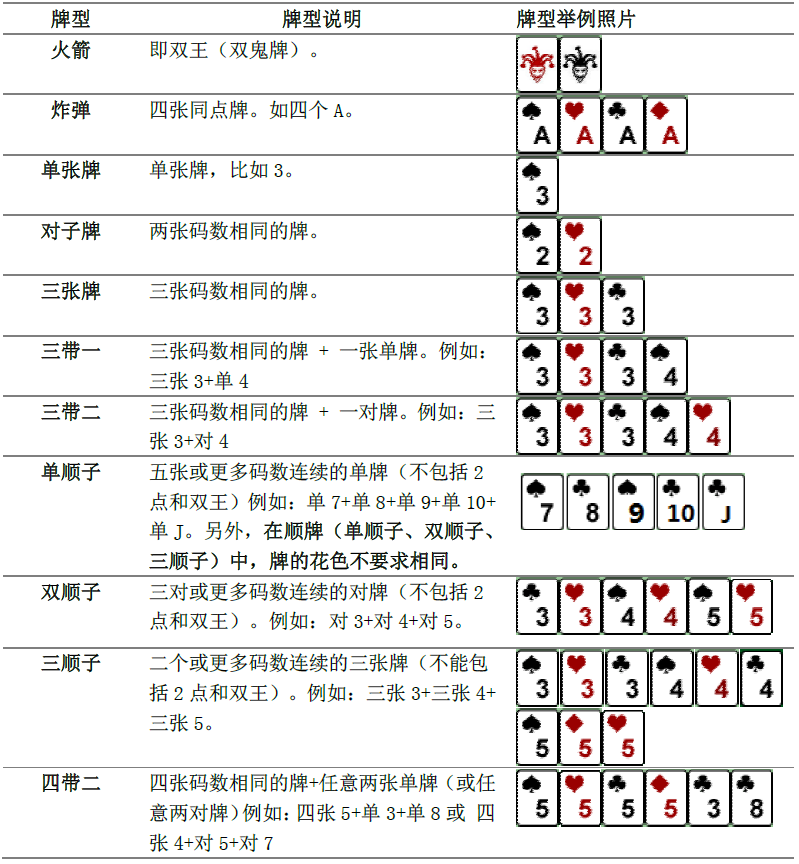
Input
第一行包含用空格隔开的2个正整数 T n ,表示手牌的组数以及每组手牌的张数。
接下来T组数据,每组数据n行,每行一个非负整数对 ai bi 表示一张牌,其中ai表示牌的数码,bi表示牌的花色,中间用空格隔开。特别的,我们用1来表示数码A,11表示数码J,12表示数码Q,13表示数码K;黑桃、红心、梅花、方片分别用1-4来表示;小王的表示方法为 0 1 ,大王的表示方法为 0 2 。
Output
共T行,每行一个整数,表示打光第i手牌的最少次数。
Sample Input Copy
输入样例#1:
1 8
7 4
8 4
9 1
10 4
11 1
5 1
1 4
1 1
输入样例#2:
1 17
12 3
4 3
2 3
5 4
10 2
3 3
12 2
0 1
1 3
10 1
6 2
12 1
11 3
5 2
12 4
2 2
7 2Sample Output Copy
输出样例#1:
3
输出样例#2:
6HINT
样例1说明
共有1组手牌,包含8张牌:方片7,方片8,黑桃9,方片10,黑桃J,黑桃5,方片A以及黑桃A。可以通过打单顺子(方片7,方片8,黑桃9,方片10,黑桃J),单张牌(黑桃5)以及对子牌(黑桃A以及方片A)在3次内打光。
对于不同的测试点, 我们约定手牌组数T与张数n的规模如下:
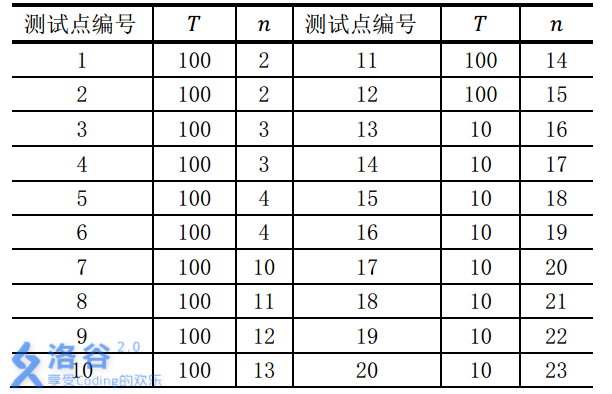
测试点编号 T n 测试点编号 T n 1 100 2 11 100 14 2 100 2 12 100 15 3 100 3 13 10 16 4 100 3 14 10 17 5 100 4 15 10 18 6 100 4 16 10 19 7 100 10 17 10 20 8 100 11 18 10 21 9 100 12 19 10 22 10 100 13 20 10 23
数据保证:所有的手牌都是随机生成的。
注:原题并未描述清楚。两张王牌不能视为对子,不能三带大王+小王,但可以四带大王+小王。四带二可以带任意两张牌,包括对子,也可以带两对牌,包括四张数码相同的牌,但不能只带一张牌。本题数据为官方数据。测试点21非官方数据。
NOIP2015提高组第一天第三题