410450: GYM104022 H Absolute Space
Description
Xiao Ming is an elementary school student. One day his math teacher instructed the students to create a series of special models, which are called "absolute space". Each model consists of many stars in the three-dimensional space and is associated with a special parameter $$$n$$$ claiming that for any star in the model, there exist exactly $$$n$$$ stars whose Euclidean distance to it is $$$1$$$.
For example, in the case of $$$n = 1$$$, you can create this model by drawing a line of length $$$1$$$, and then drawing the stars at the line's endpoints. Similarly, for $$$n = 2$$$, you can create this model by drawing a regular polygon (i.e. equilateral triangle, square and regular pentagon) with side length $$$1$$$, and then drawing the stars at the polygon's vertices. As you can see, there are infinite kinds of "absolute space".
In this class, the teacher taught them what kind of possibilities look like in the case of $$$n = 1, 2$$$, and their homework was to create a model for $$$n = 3$$$. Since the homework is too easy, Xiao Ming doesn't want to stop at these small cases. He spent a whole night reflecting on that and finally managed to find solutions applicable for any parameter $$$n$$$ $$$(= 1, 2, 3, 4, 5, \ldots)$$$. Furthermore, he found ways to shrink the number of stars when creating these models.
Such great progress brought him ecstasy, as well as insomnia. When he got up the next morning, he completely forgot how he got the idea, and his draft model had also collapsed due to the out-of-date glue he mistakenly used, so he has no proof to convince his teacher about what he has done. Could you please create a model for this poor little boy?
Given the parameter $$$n$$$, your task is to create any possible model such that the number of stars is not greater than a certain limit.
InputThe only line contains an integer $$$n$$$ $$$(1 \leq n \leq 10)$$$, indicating the parameter of the model.
OutputIn the first line, output an integer $$$m$$$ $$$(1 \leq m \leq 100)$$$, indicating the number of stars in your model.
In the next $$$m$$$ lines, output the coordinates of each star in one line, that is, output three real numbers $$$x$$$, $$$y$$$ and $$$z$$$ $$$(-100 \leq x, y, z \leq 100)$$$ in one line, representing a star at point $$$(x, y, z)$$$. Besides, it is not allowed for any two points in your output to have a Euclidean distance less than $$$0.01$$$.
To tolerate the precision error, your model will be regarded as valid if, for any star in your model, there exist exactly $$$n$$$ stars whose Euclidean distance to it is in the range $$$(0.999\,999, 1.000\,001)$$$.
1Output
2 0.000000000 0.000000000 0.000000000 1.000000000 0.000000000 0.000000000Input
2Output
3 0.000000000 0.000000000 0.000000000 1.000000000 0.000000000 0.000000000 0.500000000 0.866025404 0.000000000Input
3Output
4 0.500000000 0.000000000 -0.353553391 -0.500000000 0.000000000 -0.353553391 0.000000000 0.500000000 0.353553391 0.000000000 -0.500000000 0.353553391Input
4Output
6 0.707106781 0.000000000 0.000000000 -0.707106781 0.000000000 0.000000000 0.000000000 0.707106781 0.000000000 0.000000000 -0.707106781 0.000000000 0.000000000 0.000000000 0.707106781 0.000000000 0.000000000 -0.707106781Input
5Output
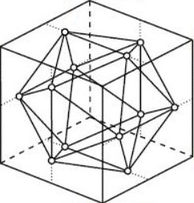
12 0.000000000 0.500000000 0.809016994 0.000000000 -0.500000000 0.809016994 0.000000000 0.500000000 -0.809016994 0.000000000 -0.500000000 -0.809016994 0.500000000 0.809016994 0.000000000 0.500000000 -0.809016994 0.000000000 -0.500000000 0.809016994 0.000000000 -0.500000000 -0.809016994 0.000000000 0.809016994 0.000000000 0.500000000 0.809016994 0.000000000 -0.500000000 -0.809016994 0.000000000 0.500000000 -0.809016994 0.000000000 -0.500000000Note
For the sample cases:
- A segment of length $$$1$$$ is a feasible model for $$$n=1$$$;
- an equilateral triangle is a feasible model for $$$n=2$$$;
- a regular tetrahedron is a feasible model for $$$n=3$$$;
- a regular octahedron is a feasible model for $$$n=4$$$;
- and a regular icosahedron is a feasible model for $$$n=5$$$ shown in the figure above.