410427: GYM104020 K Kiosk Construction

You are planning to start a Beautifully Arranged Placid Camping. You already have bought a field, which you have divided into a $$$h \times w$$$-grid of plots, and numbered them with distinct numbers $$$a_{ij}$$$ from $$$1$$$ to $$$h \cdot w$$$. However, you forgot one thing: you still need to place the reception kiosk at one of the plots. You want to minimise the maximal distance that any guest will walk from the reception kiosk to their plot. Guests will however not take the shortest path to their plot, but instead they follow the following procedure, starting at the reception kiosk:

• Look at the numbers of the four neighbouring plots.
• Go to the plot with the number closest to the destination number. In case of a tie, out of the two tying plots, go to the one with the number closest to the current plot number.
• Repeat until the destination is reached.

Note that this procedure might not terminate in some cases.

Given the numbering of the plots, find the plot number of the optimal position for the reception kiosk and the maximal walking distance to any plot from this kiosk. If, for every possible position for the reception kiosk, there is at least one plot for which the procedure outlined above does not terminate, output that this is impossible.

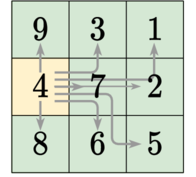
Figure 1 shows the third sample case: one solution is to put the kiosk in plot $$$4$$$, so that every other plot is at most distance $$$3$$$ away. Placing the kiosk in plot $$$7$$$ does not work as plot $$$9$$$ cannot be reached from there.

The input consists of:

• One line with two integers $$$h$$$ and $$$w$$$ ($$$2\leq h, w\leq 40$$$), the dimensions of the camping.
• $$$h$$$ lines, the $$$i$$$th of which contains $$$w$$$ integers $$$a_{i, 1}, \ldots, a_{i, n}$$$ ($$$1 \leq a_{i, j} \leq h \cdot w$$$), the plot numbers. It is guaranteed that all numbers from $$$1$$$ to $$$h \cdot w$$$ occur exactly once.

If there is a position for the reception kiosk such that every other plot can be reached, then output the optimal position for the reception kiosk and the corresponding maximal walking distance. Otherwise, output "impossible".

If there are multiple valid solutions, you may output any one of them.

2 3
1 2 3
6 5 4

2 2

3 3
1 4 8
7 5 2
3 9 6

impossible

3 3
9 3 1
4 7 2
8 6 5

4 3