410351: GYM104011 K Kaleidoscopic Route

There are $$$n$$$ cities in Kaleidostan connected with $$$m$$$ bidirectional roads. The cities are numbered from $$$1$$$ to $$$n$$$. Each road has an integer called colorfulness.

Keanu wants to travel from city $$$1$$$ to city $$$n$$$. He wants to take the shortest route — that is, the route with the smallest number of roads. Among all the shortest routes, he wants to take the kaleidoscopic one — that is, the route with the largest possible difference between the maximum and the minimum colorfulnesses of its roads. Help Keanu find such a route.

The first line contains two integers $$$n$$$ and $$$m$$$ — the number of cities and the number of roads ($$$2 \le n \le 10^5$$$; $$$1 \le m \le 2 \cdot 10^5$$$).

The $$$i$$$-th of the following $$$m$$$ lines contains three integers $$$v_i$$$, $$$u_i$$$, and $$$c_i$$$ — the indices of the cities connected by the $$$i$$$-th road, and the colorfulness of the $$$i$$$-th road ($$$1 \le v_i, u_i \le n$$$; $$$v_i \neq u_i$$$; $$$0\le c_i \le 10^9$$$).

Each pair of cities is connected by at most one road. It is guaranteed that you can travel from any city to any other city using the roads.

In the first line, print a single integer $$$k$$$ — the number of roads in the required route.

In the second line, print $$$k+1$$$ integers $$$c_0, c_1, \ldots, c_k$$$ — the sequence of cities on the route ($$$1 \le c_i \le n$$$; $$$c_0 = 1$$$; $$$c_k = n$$$).

6 8
1 5 2
5 2 5
3 5 4
1 3 10
3 4 6
4 5 7
4 6 8
2 6 1

3
1 5 4 6 

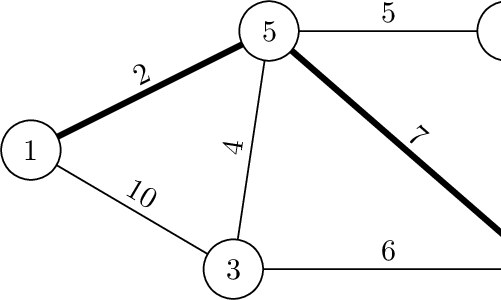
In the example test, the required route consists of $$$3$$$ roads, and the difference between the maximum and the minimum colorfulnesses of its roads is $$$8-2=6$$$.