409983: GYM103886 J Cereal Grids
Description
Envy has a cereal surplus so instead of eating his cereal, he decides he will play with them for a little bit.
Envy has $$$k$$$ distinct cereal pieces arranged on an $$$n$$$-by-$$$n$$$ grid. Each cell contains at most one piece of cereal.
In one move, Envy can shift the grid in four different ways: up, left, down and right. In a shift, all cereal pieces are moved as far as possible in the direction that they are shifted until they hit the edge of the grid or another piece of cereal.
We say a grid configuration is immobile if shifting the grid leftwards or downwards does not change its configuration.
Envy would like to know how many different immobile grid configurations he can reach by making moves some finite number of times.
Two grid configurations are considered different if any two of the same cells have different cereal pieces, or one is empty and the other contains cereal.
Because the answer can be very large, print it modulo $$$1\,000\,000\,007$$$.
InputThe first line of input contains $$$n$$$, the size of the grid $$$(1 \le n \le 1000)$$$.
The next $$$n$$$ lines of input contain $$$n$$$ characters each, where each character is either a ., meaning an empty cell, or a #, meaning it contains a cereal piece (which is distinct from all other pieces). This represents the starting grid that will be played with.
It is guaranteed that the starting grid is immobile.
OutputPrint the answer modulo $$$1\,000\,000\,007$$$.
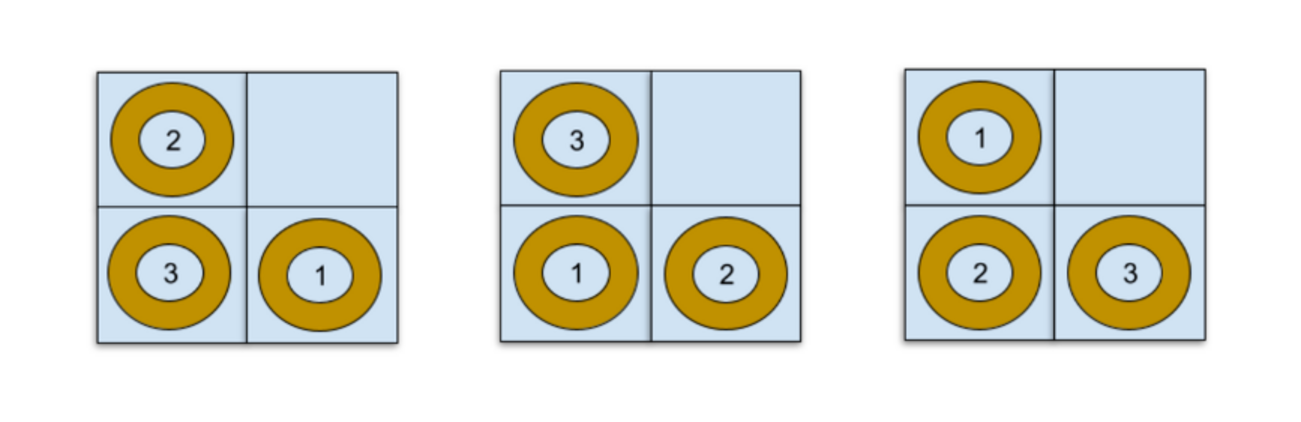
ExamplesInput2 #. ##Output
3Input
5 #.... #.... ##... ####. #####Output
21Note
In the first test, there are three possible immobile grid states (the initial state is counted) that Envy can reach from the sample case. The cereal are numbered in the visual below to differentiate one grid state from another.
Problem Credits: Mythreya Dharani