409929: GYM103855 L Make Different
Description
There are $$$N$$$ springs on a circular game board. There are two types of springs: red springs and blue springs. When the robot steps on a red spring, it can jump one spring left or right. When the robot steps on a blue spring, it can jump two springs left or right.
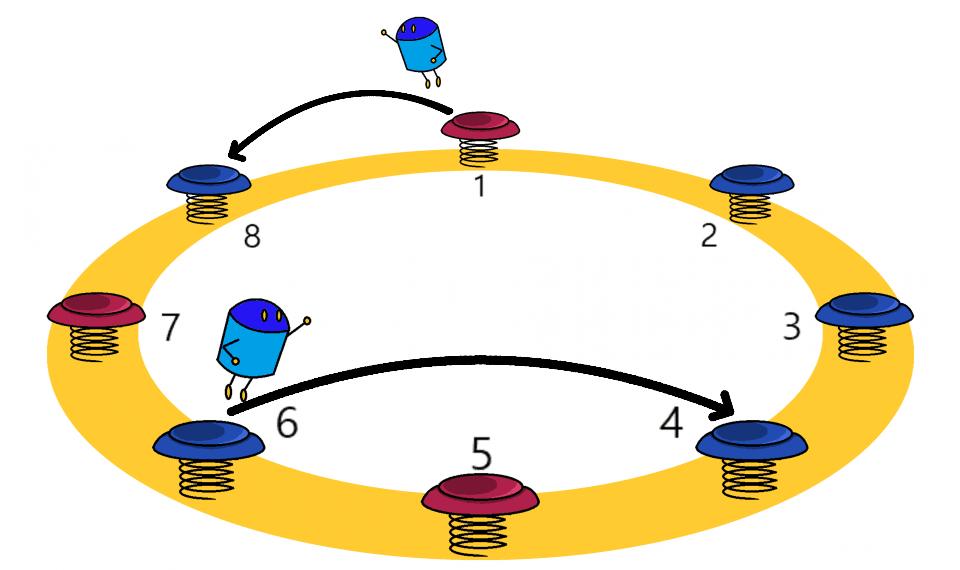 The case when the two robots are on springs 1 and 6 respectively, and a counterclockwise jump command is given.
The case when the two robots are on springs 1 and 6 respectively, and a counterclockwise jump command is given. You will play a game using two robots. In the beginning, you will place the two robots on different springs on the board. You can then issue a direction - either clockwise or counterclockwise. Both robots will jump simultaneously in the direction you command. The game ends when the robots step on springs of different colors.
You are given $$$Q$$$ queries. Each query contains the starting springs of the two robots. For each query, find the minimum number of commands needed to finish the game.
InputThe first line contains two integers $$$N$$$ and $$$Q$$$ ($$$3 \leq N \leq 100\,000$$$, $$$1 \leq Q \leq 100\,000 $$$).
The next line contains $$$N$$$ integers, the $$$i$$$-th integer denoting the type of spring $$$i$$$. Red springs are denoted by a $$$1$$$ and blue springs are denoted by a $$$2$$$.
The next $$$Q$$$ lines each contain two integers $$$p_1$$$ and $$$p_2$$$ denoting the positions at which the two robots will start the game ($$$1 \leq p_1, p_2 \leq N$$$, $$$p_1 \neq p_2$$$).
OutputOutput $$$Q$$$ lines. On the $$$i$$$-th line, output a single integer denoting the minimum number of commands required to get the two robots to land on different colored springs for the $$$i$$$-th query. If it is impossible to get the robots to land on different colored springs, output -1.
ExampleInput8 3 1 2 2 2 1 2 1 2 1 2 1 5 3 6Output
0 -1 1