409790: GYM103743 G GCD on Bipartite Graph

Given a full bipartite graph with $$$n$$$ nodes on the left and $$$m$$$ nodes on the right where any node on the left is connected to all nodes on the right. Your task is now to assign values to the nodes such that any integer $$$i \in [1,n+m]$$$ occurs exactly once and that for any cycle, the GCD (Greatest Common Divisor) of the values of all the nodes on the cycle is equal to $$$1$$$.

The GCD of some positive integers is the maximum integer that divides all the integers. For example, $$$\text{GCD}(4,6)=2$$$, $$$\text{GCD}(6,9,15)=3$$$.

The first line contains a single integer $$$T(1\le T \le 100)$$$, indicating the number of test cases.

Each test case contains two integers $$$n,m(1\le n,m \le 10^{5})$$$ in a single line. It is guaranteed that $$$\sum \max(n,m) \le 2\cdot 10^5$$$.

For each test case, if there exists a possible assignment, output YES in a single line. Then output two lines, the first of which indicates the nodes on the left, while the second of which contains the nodes on the right. If there are multiple answers, print any. The integers in each line are separated by spaces, and DO NOT PRINT ANY EXTRA SPACES at the end of each line. If you print the wrong number of elements, you will possibly get a $$$\text{Presentation Error}$$$ verdict.

If there's no possible assignment, output NO in a single line.

2
3 4
9 9

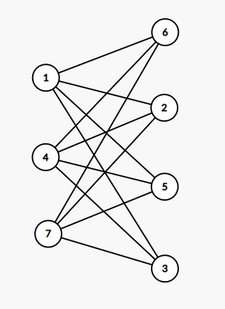
YES
1 4 7
6 2 5 3
NO

The following figure shows a correct graph with $$$n=3, m=4$$$.