409759: GYM103729 M Super Star Spectacle

Notice: The jury's solution to this problem is wrong in some cases. There exists a better solution within an acceptable time complexity. You can figure out whether your solution is better with a similar problem in NOI2007.

Karen is left alone in a solitary train car heading through a vast desert, on her journey of finding herself.

Rails in the desert can be represented as an undirected tree (i.e., have $$$n - 1$$$ railway sections connecting $$$n$$$ vertices). The glitter of Starlight splits into pieces on the rails, and Karen needs to arrange some trains to collect them all. Trains scan the rails by moving continuously along the rails and picking up pieces encountered. But pieces do move as well, even much faster. Every train can start moving or stop at any time. Trains can pick up pieces, whether they are moving or not. Here is a possible movement of some pieces and trains.

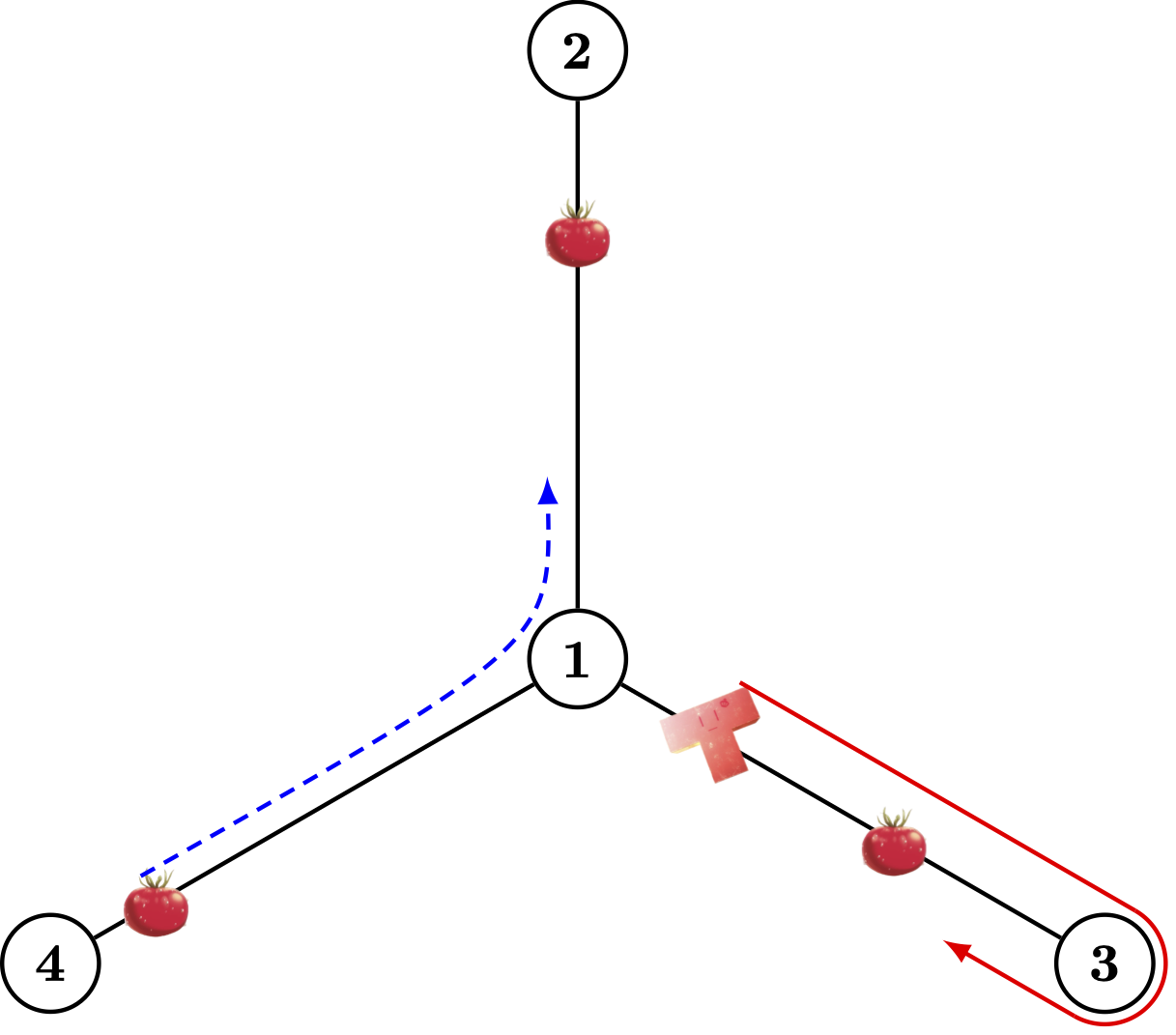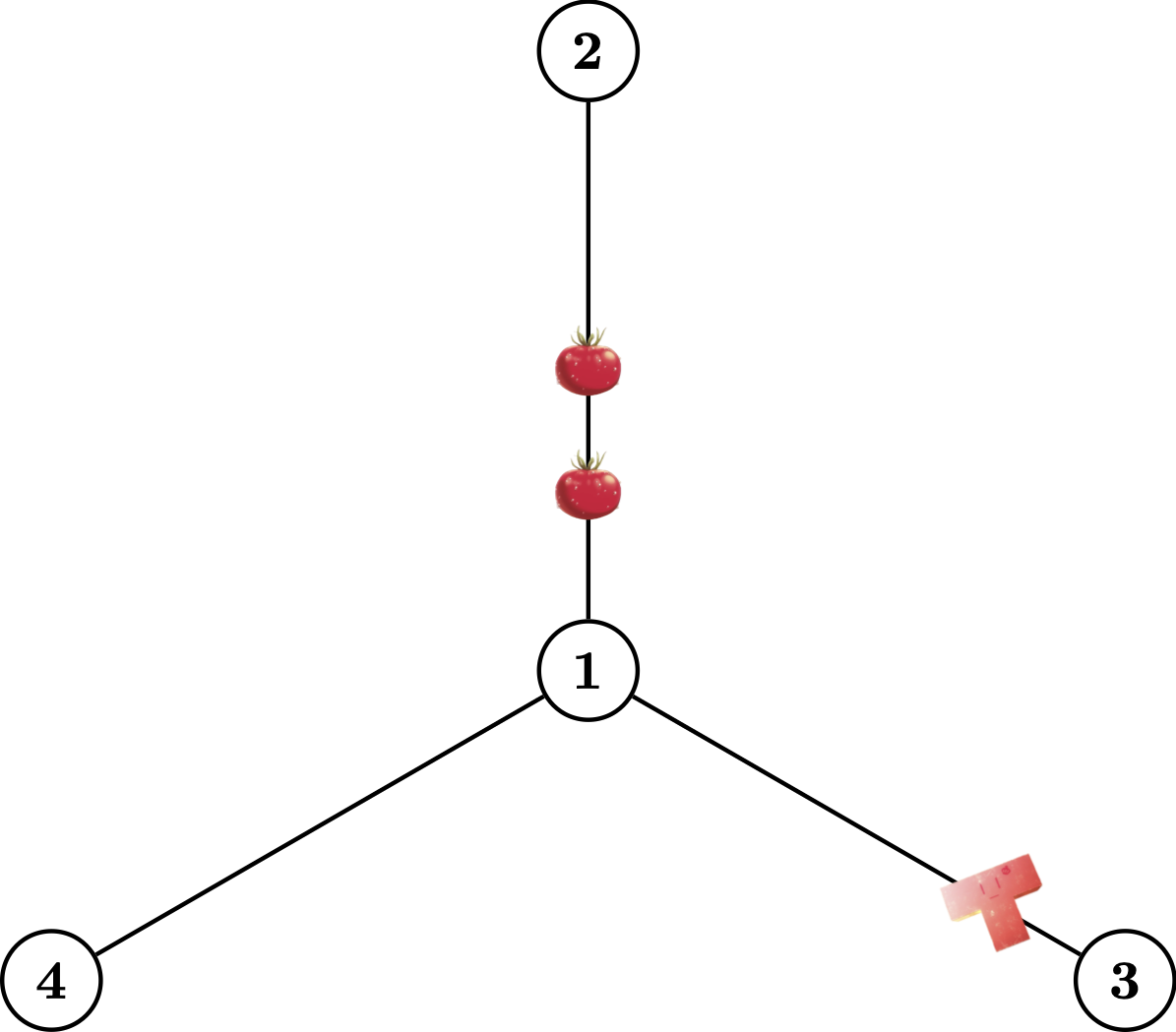The train will absolutely reach the next station, but it is questioning, both for the stages and girls. Pieces of Starlight are too tiny to locate, so it takes a number of trains and careful work to ensure no pieces are left. Please determine the minimum number of trains needed, to send Karen to the final Revue, and to send Starlight onto the next stage.

The first line contains a single integer $$$n$$$ ($$$1 \leq n \leq 3 \times 10^{5}$$$), which represents the number of vertices. Vertices are indexed from $$$1$$$ to $$$n$$$.

Each of the following $$$n - 1$$$ lines will contain two integers $$$x_i$$$, $$$y_i$$$ ($$$1 \leq x_i, y_i \leq n$$$), where $$$x_i$$$ and $$$y_i$$$ are indices of the vertices connected by the $$$i$$$-th railway section.

Print a single integer that represents the minimum number of trains needed.

4
1 2
1 3
1 4

2

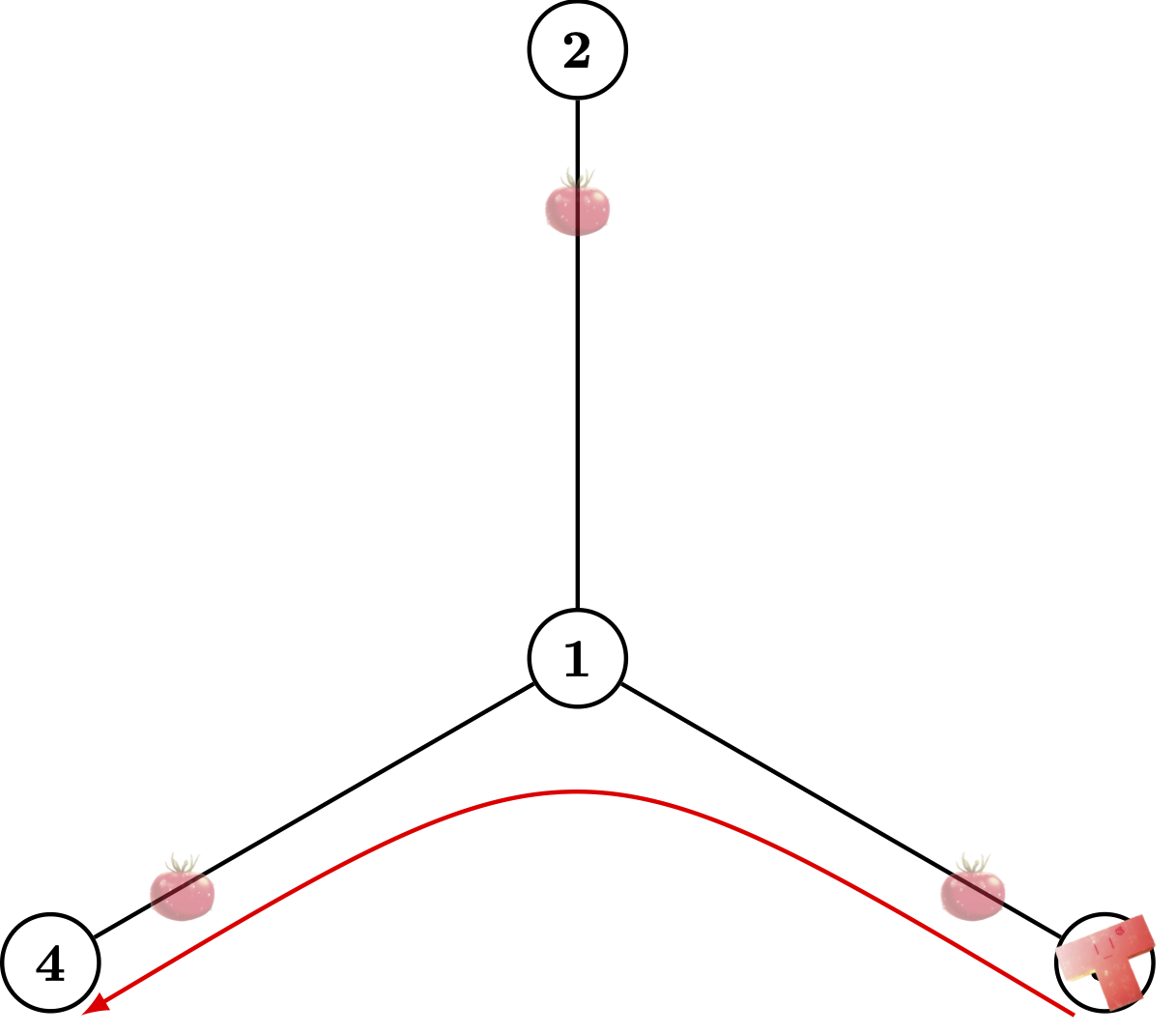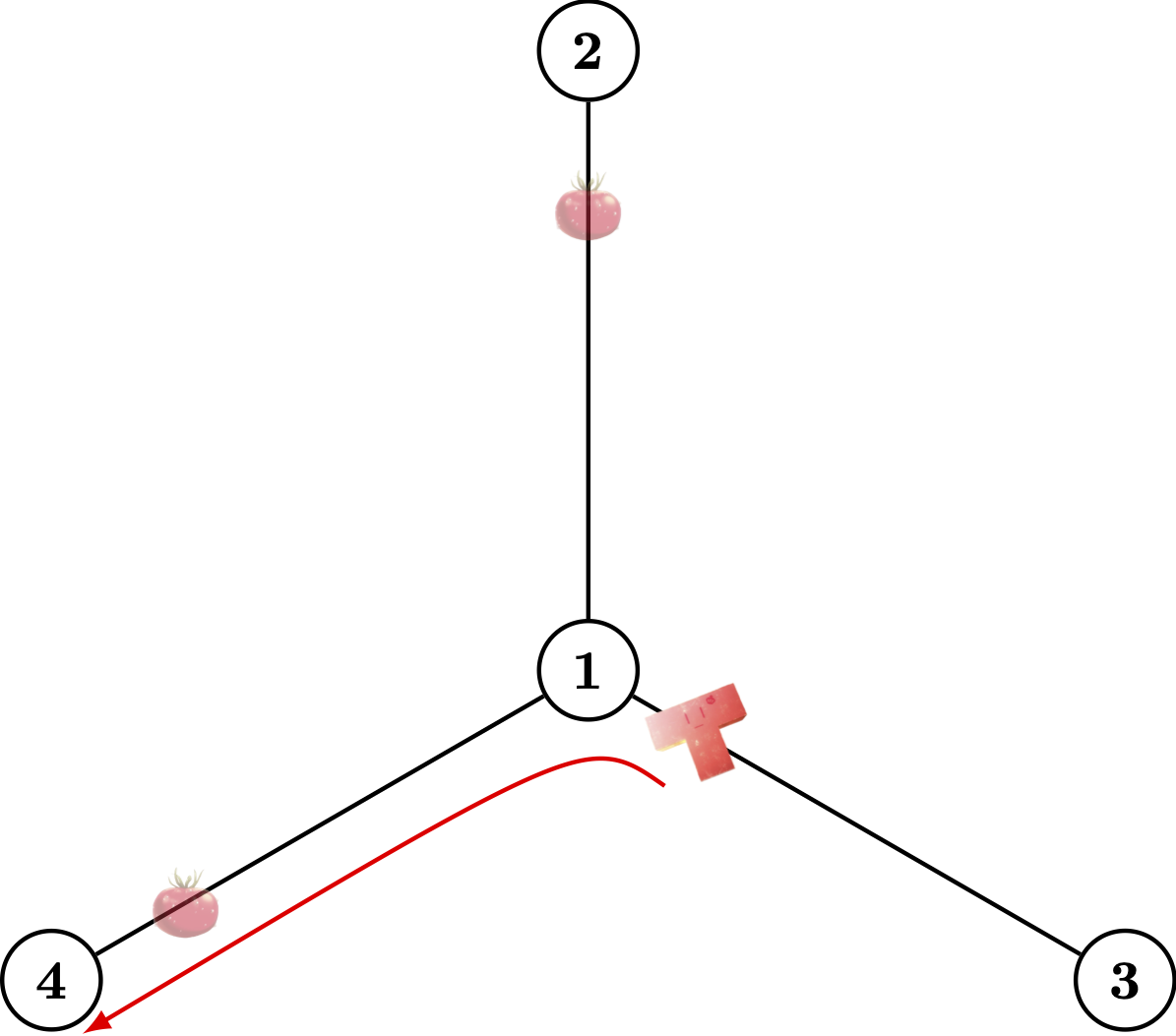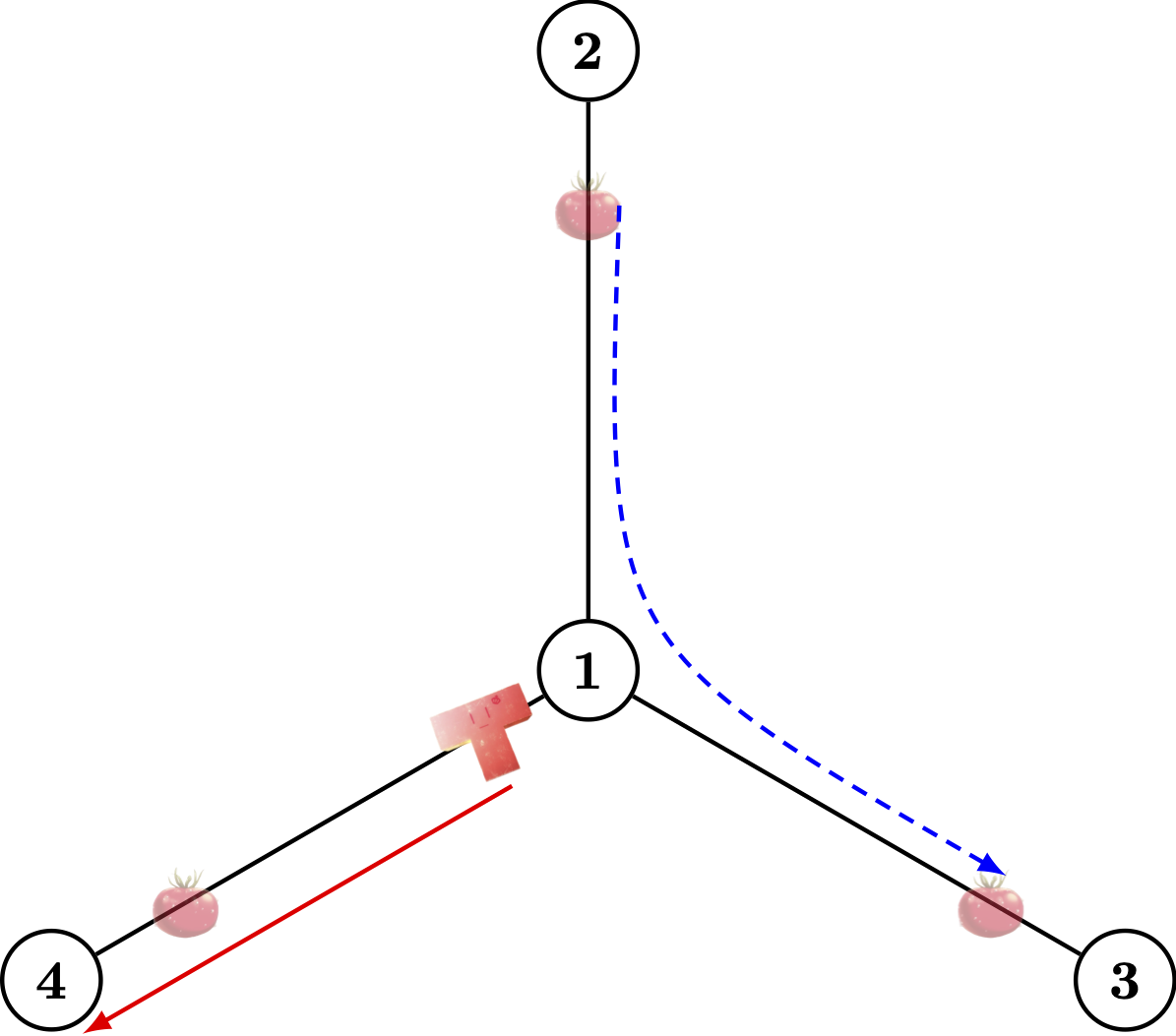In the example given, it's impossible to collect every piece with a single train. As the graphs show, the edge between (1) and (3) scanned by the train temporarily turns clear (i.e. no pieces on it). But there might always be some pieces entering it, and you could not find them. In that case, you could never determine that no pieces are left.

It's easy to construct a solution with 2 trains.