409591: GYM103640 G Generator Tree
Description
It is Christmas in Medford, Texas, and Meemaw Cooper spent a long time preparing a beautiful tree with Christmas lights in a very special configuration. But while Meemaw was outside the house, her granddaughter Missy accidentally bumped into the tree and broke the Christmas lights. Missy wants to restore the same configuration of lights before Meemaw comes back, that's why she asked for the help of her brother Sheldon who knew something about how the configuration of the lights was built.
Sheldon knew that Meemaw bought many copies of the same configuration of lights and simply put them together. A configuration of lights can be seen as a tree (undirected acyclic connected graph) in which the vertices are the lights and the edges are the wires connecting them. Each edge connects two different lights and the set of edges forms a tree. So Meemaw bought many copies of the same configuration and added some wires connecting distinct copies such that the resulting configuration was also a tree.
Sheldon quickly explained to Missy what she had to do to recover the configuration of Meemaw, and he spent the rest of the afternoon thinking about the following generalization of the problem. Given a collection of $$$N$$$ trees, determine for each tree how many other trees in the collection can generate that tree. A tree $$$T_1$$$ can generate a tree $$$T_2$$$ if it is possible to connect one or more copies of $$$T_1$$$ with edges so as to obtain a tree isomorphic to $$$T_2$$$. Note that no edge can be removed, only adding edges is allowed. Two trees are isomorphic if it is possible to label their vertices in such a way that they become exactly the same tree. For instance, a tree having edges $$$\{(1,2),(2,3)\}$$$ is isomorphic to a tree having edges $$$\{(1,3),(3,2)\}$$$.
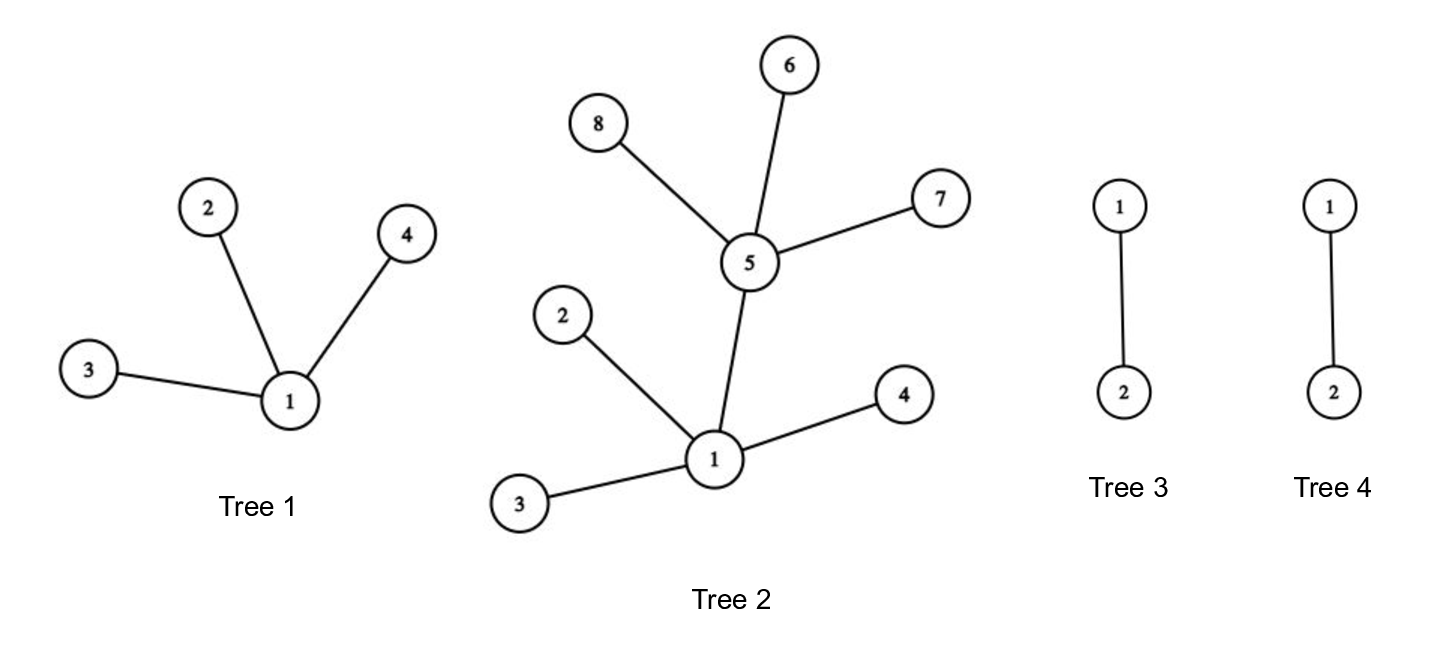
Can you help Sheldon in solving his problem? The following picture shows an example of a collection of $$$N=4$$$ trees. In this case, tree 1 cannot be generated from any other tree in the collection, tree 2 can be generated from tree 1, tree 3 can be generated from tree 4, and tree 4 can be generated from tree 3.
The first line contains an integer $$$N$$$ ($$$2 \le N \le 2 \times 10^5$$$) indicating the number of trees that Sheldon is considering. After this line, there are $$$N$$$ groups of lines, each group describing a tree.
Within each group describing a tree, the first line contains an integer $$$K$$$ ($$$2 \le K \le 2 \times 10^5$$$) representing the number of vertices in the tree. Vertices are identified by distinct integers from $$$1$$$ to $$$K$$$. Each of the next $$$K-1$$$ lines contains two integers $$$U$$$ and $$$V$$$ ($$$1 \le U,V \le K$$$ and $$$U \neq V$$$), indicating that the tree has the edge $$$(U,V)$$$.
The total amount of vertices over all the trees is at most $$$4 \times 10^5$$$.
OutputOutput a single line with $$$N$$$ integers, such that the $$$i$$$-th of them represents, for the $$$i$$$-th input tree, how many other trees in the input can generate that tree.
ExampleInput4 4 1 2 1 3 1 4 8 1 2 1 3 1 4 5 6 5 7 5 8 1 5 2 1 2 2 2 1Output
0 1 1 1