409511: GYM103604 F Kube

It's puzzle time! You're given as a present for your birthday a 3D, N-sided, coloured, puzzle and a picture of how it should look like solved.

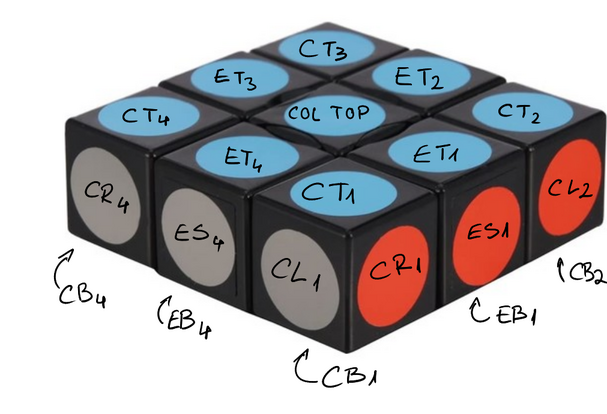
Your puzzle is composed of a center piece, N edge pieces and N corner pieces. The centre piece has 2 visible sides top and bottom that determine the top color and bottom color of the puzzle respectively. Each edge piece has 3 visible sides: top, side, and bottom. Each corner piece has 4 visible sides: top, left, right, and bottom.

The $$$side_i$$$ of the puzzle ($$$1 \leq i \leq N - 1$$$) is made of ($$$corner_i, side_i, corner_{i + 1})$$$ in this exact order. The $$$side_n$$$ of the puzzle is made of ($$$corner_n, side_n, corner_1$$$) in this exact order.

The only move you have in your arsenal to solve the puzzle is $$$twist_i$$$ ($$$1 \leq i \leq N$$$), which rotates the $$$i$$$th side $$$180^\circ$$$. Performing this move would cause the following: both corner pieces would swap place, the top side and bottom side of both the corner pieces and the edge piece will be swapped, and the sides of both corner pieces will be swapped. That is, if you performed $$$twist_i$$$, where $$$side_i$$$ is ($$$c_{i1}, e_i, c_{i2}$$$), you get ($$$c_{i2}', e_i', c_{i1}'$$$), where: if $$$c_i = (t, l, r, b)$$$, $$$c_i' = (b, r, l, t)$$$ and if $$$e_i = (t, s, b)$$$, $$$e_i' = (b, s, t)$$$.

The solved puzzle:

• has $$$N + 2$$$ different colours on it: the top, the bottom, and each of the N sides.
• for each side face: the left corner's right, the side piece's side and the right corner's left have the same colour (each side has a solid color). The top sides of all 3 pieces have the colour of the top side of the puzzle. The bottom sides of all 3 pieces have the colour of the bottom side of the puzzle (i.e. all top sides form a solid colour and all bottom sides form a solid colour).

Given the initial state of all the pieces, your task is to say if there is a solution for the puzzle, and if so output a solution that leads you to the solved state.

The first line of the input contains $$$N$$$ ($$$4 \leq N \leq 100$$$), the number of sides of the puzzle.

The following line contains two integers col_top and col_bot, the colours of the top side of the puzzle and the colour of the bottom side of the puzzle respectively ($$$0 \leq col\_top,\ col\_bot \leq N + 1,\ col\_top \ne col\_bot$$$).

Each of the following $$$N$$$ lines contains a tuple ($$$ct_i, cl_i, cr_i, cb_i$$$) the top colour, the left colour, the right colour and the bottom colour for the $$$i$$$th corner ($$$0 \leq ct_i,\ cl_i,\ cr_i,\ cb_i \leq N + 1$$$).

Each of the followin $$$N$$$ lines contains a tuple ($$$et_i, es_i, eb_i$$$) the top colour, the side colour and the bottom colour of the $$$i$$$th edge ($$$0 \leq et_i,\ es_i,\ eb_i \leq N + 1$$$).

It is guaranteed that the set {$$$col\_bot,\ col\_top,\ es_1,\ es_2,\dots\ ,es_n$$$} = {$$$0,\ 1,\ 2,\dots\ ,\ n + 1$$$}. Obviously the order of the elements can differ.

If there is no solution you should output a single line containing the integer -1.

If there is a solution you should output two lines. The first line will contain an integer $$$k$$$, the number of moves in your solution. The following line will contain $$$k$$$ integers $$$t_1, t_2,\dots\ , t_k$$$, the twists performed on the puzzle to solve it ($$$1 \leq t_i \leq N$$$). If $$$t_i$$$ appears in your solution, it means that the $$$i$$$th move you made was a twist of the $$$t_i$$$th side of the puzzle.

Note that the MAXIMUM admitted $$$k$$$ is $$$10^5$$$.

4
0
5
5 4 3 0
0 1 2 5
0 2 3 5
5 1 4 0
0 1 5
0 2 5
5 3 0
0 4 5

5
1 2 3 2 1

For an input with $$$N = 4$$$ this is how the solved state would look like: