409505: GYM103585 L Perfect Cacti: Part 2

There are two parts for this problem. This is Part 2, which extends on the problem given in Part 1. Please read Part 1 first for the problem details.

Cacti are basically desert trees, and they deserve some love too.

After staring at a bunch of cacti, you've realized that, indeed, cacti are quite beautiful! In fact, as you looked at them more, you realize that some "perfect cacti" look geometric:

After studying cacti for a bit longer, you've finally been able to come up with this construction for a perfect $$$k$$$-cactus of height $$$h$$$:

1. Start with a regular polygon with $$$k$$$ edges, and designate a root vertex.
2. If this is cactus has a height $$$h > 1$$$, then each non-root vertex of this polygon grows a $$$k$$$-cactus of height $$$h-1$$$, where the sub-cacti are rooted at the point they grew from.

Based on this definition, the cactus shown above is a $$$3$$$-cactus of height 3.

With this more general definition of $$$k$$$-cacti of height $$$h$$$, can you solve the same set of queries?

The first line begins with three integers, $$$k$$$ $$$(3 \leq k \leq 10^{18})$$$, $$$h$$$ $$$(1 \leq h \leq 10^{18})$$$ and $$$q$$$ $$$(1 \leq q \leq 10^5)$$$. $$$k$$$ and $$$h$$$ describe the cactus graph (which is a $$$k$$$-cactus of height $$$h$$$).

It is guaranteed that the number of nodes in the perfect cactus graph does not exceed $$$10^{18}$$$.

Then, $$$q$$$ lines follow, each containing three integers: $$$a, i, j$$$. The type of query is determined by $$$a$$$:

• $$$a=1$$$: Find the minimum number of edges needed to get from vertex $$$i$$$ to vertex $$$j$$$.
• $$$a=2$$$: Remove the edge from vertex $$$i$$$ to vertex $$$j$$$. It is guaranteed that this edge exists in the perfect cactus graph.
• $$$a=3$$$: Restore the edge from vertex $$$i$$$ to vertex $$$j$$$. It is guaranteed that this edge used to exist in the perfect cactus graph, but is currently not in the graph.

Since the graph is not directly given to you, the vertices are indexed in the following way. For each polygon, number the vertices $$$0 \ldots k-1$$$, starting at the root and moving in clockwise order. Each index $$$i$$$, when parsed as a base $$$k$$$ number, can be interpreted as a path, where each digit corresponds to a vertex in the polygon to move to. See the notes below for details.

Also, note that the numbering convention given in Part 1 is the $$$h=1$$$ case of the above numbering.

For each query where $$$a=1$$$, print out the minimum number of edges needed to get from vertex $$$i$$$ to vertex $$$j$$$. If no path exists, output -1.

10 1 7
1 0 8
2 0 9
1 0 8
2 0 1
1 0 8
3 0 9
1 0 8

2
8
-1
2

3 3 11
1 13 22
2 1 2
2 3 13
1 13 22
2 0 1
1 13 22
1 13 17
3 0 1
1 13 22
2 0 2
1 13 22

5
7
-1
4
7
-1

The perfect cactus in the problem description is numbered as follows. The red numbers are the vertex labels in the polygon, the blue numbers are the index of each vertex, written in base 3.

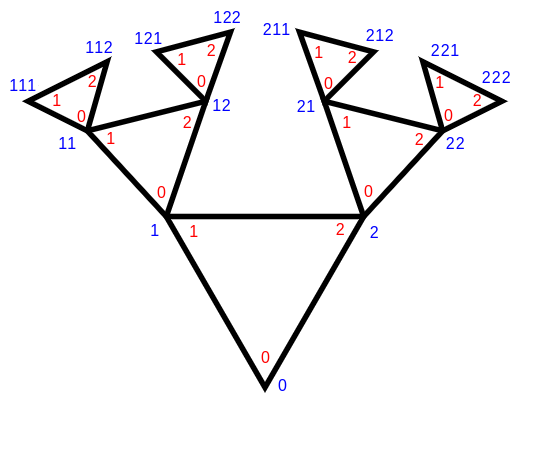
For example, the vertex labelled $$$17 = 122_3$$$ corresponds to starting at the root, moving to vertex 1 in the polygon, then moving to vertex 2 in the next polygon, and then finally moving to vertex 2 in the final polygon.