409401: GYM103496 N Nene is You

N. Nene is Youtime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard output

Cindy was going through her old hard drives and found pictures of herself from when she was in Grade 2. Oh my gosh! She looked so nene in these old pics! Nene is a Tagalog slang word used to refer to the childish appearance of young girls, with the additional connotation of such things being baduy (lame or unfashionable, particularly due to being out of style).

The picture is encoded in a pixelmap, and can be represented by a grid of characters with $$$r$$$ rows and $$$c$$$ columns. The color of each pixel is represented by an uppercase English letter. In order to reduce the nene-ness of her picture, Cindy opened it in her favorite image-editing software Inkekescape, which only has one type of operation. When Cindy says, x is y (where x and y are uppercase English letters), the program replaces all pixels of color x (if any) with pixels of colors y.

Cindy has already performed $$$n$$$ such operations on her picture. But then, she's starting to have second-thoughts. She realizes that being nene (or totoy, for boys) was a phase that everyone went through, so she has nothing to be ashamed of. In fact, now she wants to preserve the original picture so that she has an authentic record of her childhood memories.

Unfortunately, she saved over the original copy of the picture, with no backup. The only way Cindy can fix her photo now is by using more of the x is y operations of Inkekescape.

Given the $$$n$$$ operations that Cindy has already performed, is it possible to perform some more operations to recover the colors of her original picture? If yes, please actually provide the series of operations that accomplishes this goal.

Input

The first line of input contains two space-separated integers $$$r$$$ and $$$c$$$, the number of rows and the number of columns in the picture.

Then, $$$r$$$ lines follow, each containing a string of $$$c$$$ characters. This encodes the picture.

Then, this is followed by a line with a single integer $$$n$$$, the number of operations.

Then, $$$n$$$ lines follow, each containing the words x is y, where x and y are uppercase letters. These are the operations that Cindy had already performed, in the order that she performed them.

Output

If the task is possible, output a single line containing the word YES; otherwise, output NO.

If YES, output another line containing a single integer $$$m$$$, the number of extra operations that you wish to perform. Then, output $$$m$$$ lines, each containing the words x is y, where x and y are uppercase letters. This corresponds to the extra operations, in the order that you wish to perform them, done after Cindy's last operation. After the last operation is done, the photo should be restored to its original state.

We can show that given the constraints, if a solution exists, there is one that satisfies $$$0 \leq m \leq 10^5$$$. If there are multiple solutions, output any of them that have $$$m$$$ in this range. Note that you don't have to minimize $$$m$$$.

Scoring

$$$$$$\begin{align*}

&\begin{array}{|l|} \hline \text{Constraints For All Subtasks} \\ \hline 1 \leq r \times c \leq 10^5 \\ 1 \leq n \leq 10^4 \\ \hline \end{array}\\

&\begin{array}{|c|c|l|} \hline \text{Subtask} & \text{Points} & \text{Constraints} \\ \hline 1 & \mathbf{20} & \text{All pixels in the initial grid are the same color.} \\ \hline 2 & \mathbf{20} & \text{There are at most three different-colored pixels in the initial grid.} \\ \hline 3 & \mathbf{20} & \text{$1 \leq r \times c \leq 64$} \\ && \text{$1 \leq n \leq 100$} \\ \hline 4 & \mathbf{20} & \text{$1 \leq r \times c \leq 1600$} \\ && \text{$1 \leq n \leq 100$} \\ \hline 5 & \mathbf{20} & \text{No further constraints.} \\ \hline \end{array}\\

\end{align*}$$$$$$

ExamplesInput

3 2
AA
AA
AA
2
A is B
B is A

Output

YES
0

Input

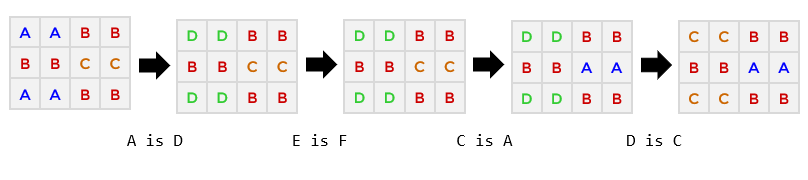
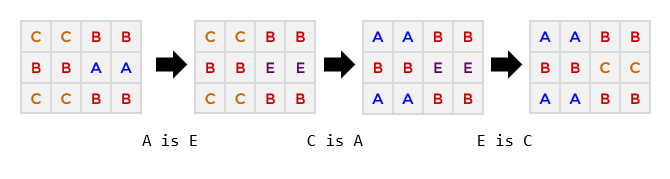
3 4
AABB
BBCC
AABB
4
A is D
E is F
C is A
D is C

Output

YES
3
A is E
C is A
E is C

Input

1 3
ABC
2
A is D
C is D

Output

NO

Note

For the first sample input, Cindy's operations already restored the photo to its original state, so we don't have to do anything.

We illustrate the second sample input. Here are the operations performed by Cindy. Note that the E is F operation did nothing, because there were no E pixels at the time.

We can restore this photo to its original state. For example, consider the following series of operations.