409398: GYM103496 K Kaleidoscope World

Bob took an internship under the famous Filipino game designer Francisco Marikina (or Francisco M for short). Francisco M's goal is to revolutionize the Original Pilipino MMO (OPM) genre. Francisco M's first big decision is to have the game take place on a grid, instead of being free-roaming. But what kind of grid?

• First, he thought of using triangles, but then he would have to make it out of Bamboo, which isn't sturdy enough.
• Second, he thought that it was Hip to Be Square, but then realized it doesn't fit his overall theme of OPM.
• Thus, Francisco M realized his only option was to use a hexagonal grid for his game, to represent a Kaleidoscope World.

Francisco M's game takes place on an infinite hexagonal grid called the kaleidoscope world. A special hexagon has been marked as the starting city.

All hexagons are oriented such that they have two horizontal sides. In one step, a player can travel from their current hexagon to the hexagon that is directly up, down, right-up, right-down, left-up, or left-down from their position, represented by the shortcuts U, D, RU, RD, LU, LD, respectively. See the following diagram.

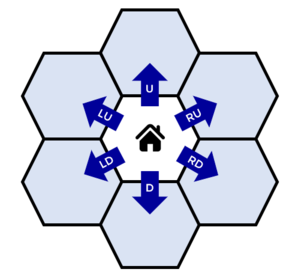
Players begin at the starting city. To move around, players choose a direction $$$t$$$ and a positive integer $$$k$$$, then move $$$k$$$ steps in that direction. The path of a player is a sequence of such movements.

Francisco M has traced the paths of $$$n$$$ different beta testers in his game. His task for Bob is to construct the following widget. Given two different players, Bob's widget should be able find the distance between those two players' final positions. The distance between two hexagons in the kaleidoscope world is equal to the minimum number of single steps needed to travel from one hexagon to the other. Bob's widget will also be tested against $$$q$$$ different queries.

Bob was quite proud of his solution, and challenges you to replicate his success.

The first line of input contains a single integer $$$n$$$, the number of players.

Each player is then described in the following manner.

• First, a line containing a single string, the player's username.
• Then, a line containing a single integer $$$m$$$, the number of movements made by this player.
• Then, $$$m$$$ lines follow, each of the form t k, where $$$t$$$ is one of U, D, RU, RD, LU, LD and $$$k$$$ is a positive integer, corresponding to the direction and number of steps of that movement. These movements are given in the same order that they are performed by this player.

The next line of input contains a single integer $$$q$$$, the number of queries.

Then, $$$q$$$ lines follow, each describing a query. Each line contains two space-separated strings, corresponding to the usernames of two different players.

For each query, output a line containing a single integer, the distance between the final positions of the two players in that query.

$$$$$$\begin{align*}

&\begin{array}{|l|} \hline \text{Constraints For All Subtasks} \\ \hline 2 \leq n \leq 2000 \\ \text{Each player's username is at most nine characters long, and consists only of upper or lowercase letters, or digits.} \\ \text{No two players have the same username.} \\ \text{$1 \leq m \leq 10$ for all players.} \\ \text{$1 \leq k \leq 10^7$ for all movements.} \\ 1 \leq q \leq 10^4 \\ \text{The two usernames in each query are different.} \\ \text{Each username mentioned in the queries belongs to some player given in the input.} \\ \hline \end{array}\\

&\begin{array}{|c|c|l|} \hline \text{Subtask} & \text{Points} & \text{Constraints} \\ \hline 1 & \mathbf{20} & \text{$t$ is }\mathtt{U}\text{ or }\mathtt{D}\text{ for all movements} \\ \hline 2 & \mathbf{30} & \text{$m = 1$ for all players} \\ \hline 3 & \mathbf{30} & \text{$k \leq 3$ for all movements} \\ \hline 4 & \mathbf{20} & \text{No further constraints.} \\ \hline \end{array}\\

\end{align*}$$$$$$

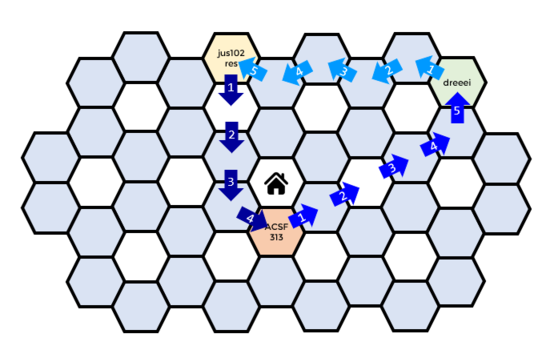
3
jus102res
2
U 2
LU 1
dreeei
1
RU 4
ACSF313
3
LD 2
RD 2
U 1
3
ACSF313 dreeei
jus102res ACSF313
jus102res dreeei

5
4
5

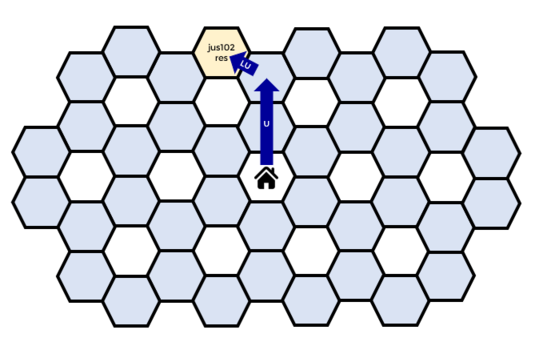
Here is the path taken by jus102res.

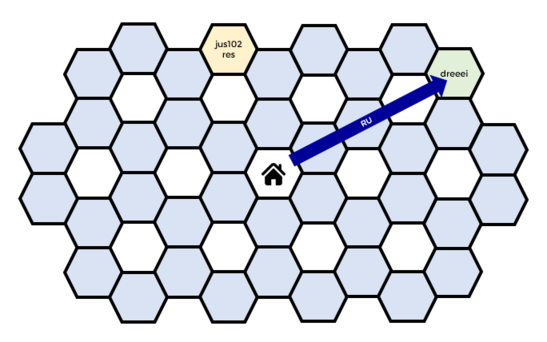
Here is the path taken by dreeei.

Here is the path taken by ACSF313.

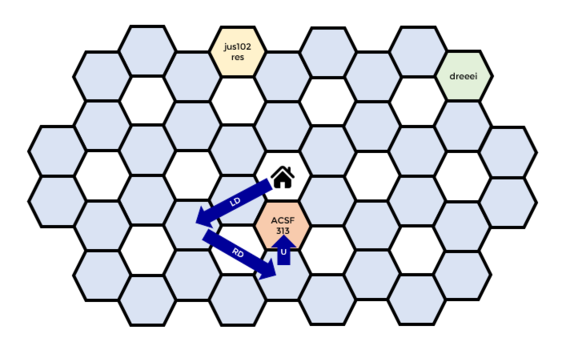
We also illustrate the lengths of the shortest paths between each of the players, giving the answer to each of the queries above.