409154: GYM103447 F Master Spark
Description
You are playing Touhou Impershiable Night, a bullet curtain shooting game, and are fighting against Kirisame Marisa, the boss in stage 4B, who launchs master sparks to attack players. Following is a illustration of this scene.
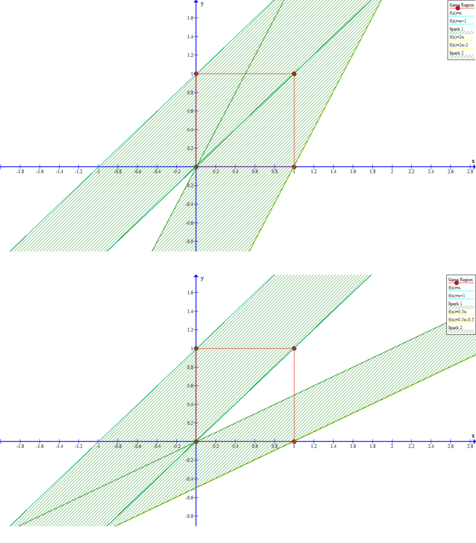
Image that the game area is in a 2D plane. The player is restricted in a rectangle region $$$M~(\{(x,y) \; | \; 0\le x \le X, 0\le y \le Y\})$$$ and the sparks can be described as ribbon regions $$$S_i~(\{(x,y) \; | \; C_i \le A_ix + B_iy \le D_i\})$$$.
Now given $$$X,Y$$$ and $$$n$$$ sparks $$$S_1, S_2, \cdots, S_n$$$, you want to know that if there exists such a point $$$P~(P \in M)$$$ that $$$\forall i \in \{1, 2, \cdots, n\}, P \notin S_i$$$ to avoid all sparks and autowin the game.
InputThe first line contains one integer $$$T~(1\le T \le 2000)$$$, denoting the number of test cases.
For each test case:
The first line contatins three integers $$$X,Y,n~(1\le X,Y \le 1000, 1\le n\le 2000)$$$, denoting the size of the game region and the number of sparks.
Following $$$n$$$ lines each contains four integers $$$A, B, C, D~(|A|, |B|, |C|, |D| \le 1000, A^2+B^2 > 0, C \le D)$$$, denoting the parameters of given sparks.
It's guaranteed that $$$\sum n \le 2000$$$.
OutputOutput one $$$01$$$-string $$$S$$$ of length $$$T$$$ in one line where $$$S_i = 1$$$ iff such autowinning point exists in case $$$i$$$ while $$$S_i = 0$$$ iff no such points.
ExampleInput2 1 1 2 1 -1 -1 0 2 -1 0 2 1 1 2 1 -1 -1 0 1 -2 0 1Output
01Note
Following are the illustrations of two sample cases.