409136: GYM103446 A Strange Functions

Given $$$n$$$ functions $$$f_1(x), f_2(x), \cdots, f_n(x)$$$, where $$$$$$ f_i(x) = \left\{ \begin{aligned} |\arctan(k_i\sec(x - a_i))| \; & \; (x \neq a_i + (k+\frac{1}{2})\pi \, (k = 0, \pm 1, \pm 2, \cdots)) \\ \frac{\pi}{2} \; & \; (x = a_i + (k+\frac{1}{2})\pi \, (k = 0, \pm 1, \pm 2, \cdots)) \end{aligned} \right. $$$$$$

For each function $$$f_i(x)$$$, determine if there is an $$$x_i$$$ that $$$\forall j \in \{1, 2, \cdots, i-1, i+1, \cdots, n\}, f_i(x_i) < f_j(x_i)$$$.

Note that:

• "$$$\arctan$$$" is the inverse function of "$$$\tan$$$".
• $$$\sec (x) = \frac{1}{\cos(x)}$$$.

The first line contains one integer $$$n\,(1 \le n \le 10^5)$$$, denoting the number of given functions.

Following $$$n$$$ lines each contains two integers $$$k_i, a_i \, (1 \le k_i \le 10^5, |a_i| \le 10^5)$$$, denoting the given functions.

It is guaranteed that $$$\forall 1 \le i < j \le n, \; k_i \neq k_j \; \mathrm{or} \; a_i \neq a_j$$$.

Output one line containing one $$$01$$$-string $$$S$$$ of length $$$n$$$, where $$$S_i = 1$$$ iff such $$$x_i$$$ exists, or $$$S_i = 0$$$.

3
1 1
3 2
2 3

101

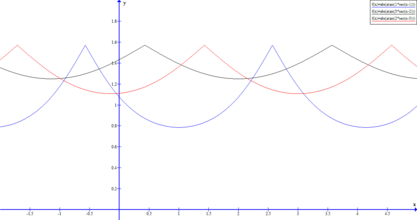
Here is an illustration for the sample case.