409113: GYM103439 E Flood Fill
Description
Given are two black and white $$$N \times M$$$ images $$$A$$$ and $$$B$$$.
The "flood fill" tool works as follows: you choose any cell $$$(x, y)$$$, locate its connected component and flip the colors of all the cells in the component (if the cell was black, it becomes white, and if it was white, it becomes black). The connected component of the cell is the set of cells you can reach by going up/down/left/right without changing color.
You can apply the "flood fill" tool to image $$$A$$$ any number of times. What is the minimum number of cells in which $$$A$$$ can be different from $$$B$$$ after some sequence of operations?
InputThe first line of input contains two integers $$$N$$$ and $$$M$$$ ($$$1 \le N, M \le 100$$$) — the dimensions of the images.
Each of the next $$$N$$$ lines contains a binary string of length $$$M$$$, describing the corresponding row of the image $$$A$$$.
Each of the next $$$N$$$ lines contains a binary string of length $$$M$$$, describing the corresponding row of the image $$$B$$$.
Here 0 corresponds to the cell colored white, 1 corresponds to the cell colored black.
OutputOutput a single integer — the minimum possible number of cells in which $$$A$$$ can be different from $$$B$$$ after some sequence of operations.
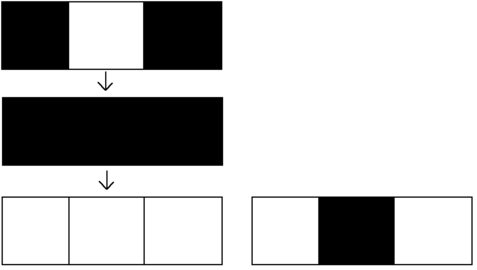
ExamplesInput1 3 101 010Output
1Input
4 4 0001 0101 0101 0111 0000 1110 1110 1110Output
7Note
In the first example, you can apply the tool to the middle cell twice. This way, two images will differ only in $$$1$$$ cell.
In the second example, you can just make the entire image black. This way, two images will differ in $$$7$$$ cells.
