409035: GYM103423 B Vacuum Cleaner
Description
' In the civil court of the Mayan emperor, lived a prophet. And this prophet prophesied that "The difference is made by the man who is motivated in every what he did is no longer valid tomorrow a take from 0 will prove that again the best". Now, unfortunately, he neither knew nor was he aware of.
Anyway, the Hagii, aka the Hagï, is once again facing the demotion of the Trecutul. And now, he is watching the decisive match against his rival, FCSpreB. The more exact problem he's facing is this:
A football game is being played on a football pitch of infinite dimensions. For simplicity, you can think of this space as an xOy Cartesian plane.
It has $$$N$$$ ($$$1 \le N \le 100\,000$$$) pairs of players points, which can be described by triplets of the form $$$(x_1,x_2,y)$$$. This means that on the football field where the match is currently taking place, there is a player at position $$$(x_1,y)$$$ who wants to pass to the player at position $$$(x_2,y)$$$.
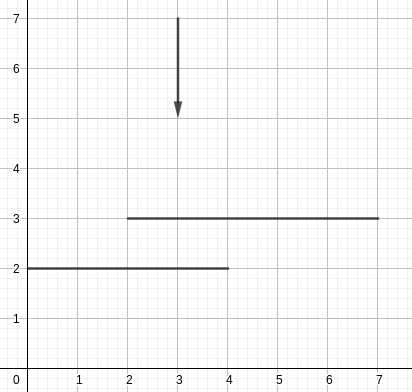
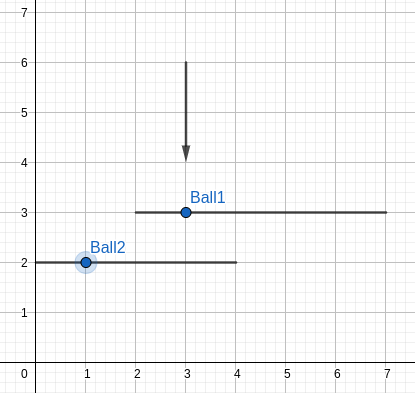
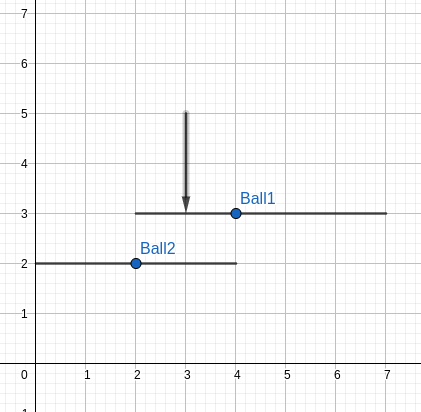
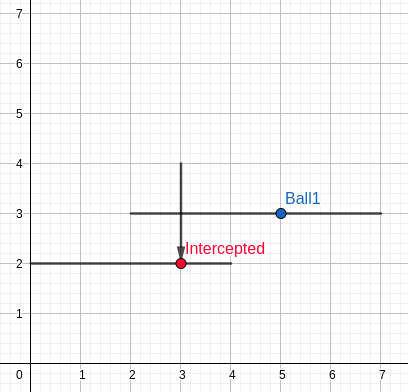
Except that this is where Gigi the Bo$$ comes in. He has $$$K$$$ ($$$1 \le K \le 100\,000$$$) players, with very wide legs. Specifically, each player can be described by a triplet of numbers $$$(x,y_1,y_2)$$$, meaning that at time $$$T=0$$$, this player blocks all points on the segment bordered by the points $$$(x,y_1)$$$ and $$$(x,y_2)$$$. Thus, at time $$$t$$$, he will block all points between $$$(x,y_1-t)$$$ and $$$(x,y_2-t)$$$ (One can visualize the players strolling downwards with speed = 1 (oY unit) / (time unit)).
We say that a pass $$$(a,b,y)$$$ is successful if for any natural $$$a \le x \le b$$$, we have that at time $$$x-a$$$ the position $$$(x,y)$$$ is not blocked by any segment. One can visualise this process as if a player at position $$$(a,y)$$$ shoots a ball towards $$$(b,y)$$$ with speed = 1 (oX unit) / (time unit).
 |  |  |  | 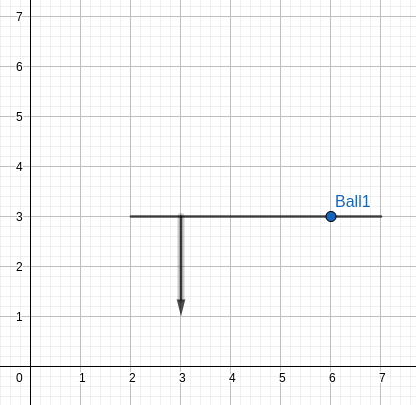 | 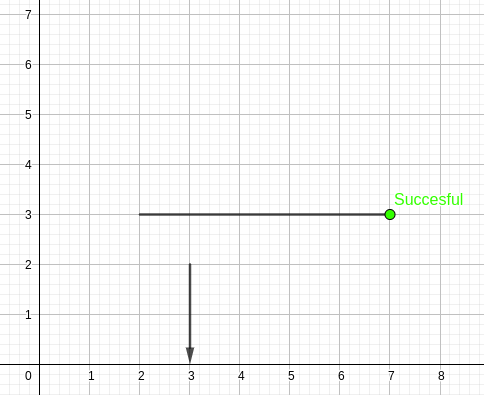 |
Now, the Hagii, a.k.a. the Hagï, knows all this data, but he is busy cleaning up the football field with the vacuum cleaner. So he gives you the data, and asks you which of his passes will be succesful.
InputFirst line of input contains the $$$N$$$ and $$$K$$$ of the input (in this order). On each of the following $$$N$$$ lines there will be a triplet described by $$$(x_{1_i},x_{2_i},y_i)$$$, each of them describing a pair of players of Hagii's. We guarantee that $$$x_{1_i} \le x_{2_i}$$$
On the following $$$K$$$ lines, there will be a triplet described by $$$ (x_i,y_{1_i},y_{2_i}) $$$ , each of them describing a player of Gigi's. We guarantee that $$$y_{1_i} \le y_{2_i}$$$
OutputFor each pair of players of Hagii's, print either 1, if the pass is successful, or 0, if the pass is unsuccessful.
Scoring| Group | Add. constraints | Points | Req. groups | |||
| $$$N$$$ | $$$K$$$ | Special constraints | ||||
| $$$1$$$ | $$$N \le 1\,000$$$ | $$$N \le 1\,000$$$ | — | $$$10$$$ | — | |
| $$$2$$$ | $$$N \le 100\,000$$$ | $$$K \le 100\,000$$$ | There are no players will eventually block the same point on the Ox line (i.e. for each pairs of players of Gigi's, their corresponding $$$x$$$ values are different) | $$$40$$$ | — | |
| $$$3$$$ | $$$N \le 100\,000$$$ | $$$N \le 100\,000$$$ | — | $$$50$$$ | — | |
It is guaranteed that for all tests, we have:
- $$$1 \le x_i, x_{1_i}, x_{2_i}, y_i, y_{1_i},y_{2_i} \le 200\,000$$$
- $$$x_{1_i} \le x_{2_i}, y_{1_i} \le y_{2_i}$$$
4 3 1 6 4 2 6 4 1 3 7 2 3 6 6 7 8 3 6 6 2 6 7Output
0 0 1 0Input
5 5 5 7 7 1 8 9 8 9 17 2 4 10 1 10 9 7 11 16 4 7 14 3 4 13 8 11 11 3 9 13Output
1 0 1 0 0Note
For the first example:
The pass defined at the beginning of (1 6 4) is blocked by the player defined at the beginning of (3 6 6) at time 2
The pass defined at the beginning of (2 6 4) is blocked by the player defined at the beginning of (6 7 8) at time 4
The pass defined at the beginning of (1 3 7) is not blocked by any player
The pass defined at the start of (2 3 6) is blocked by the player defined at the start of (2 6 7) at time 0
For the second example:
The pass defined at the beginning of (5 7 7) is not blocked by any player
The pass defined at the beginning of (1 8 9) is blocked by the player defined at the beginning of (3 4 13) at time 2
The pass defined at the beginning of (8 9 17) is not blocked by any player
The pass defined at the start of (2 4 10) is blocked by the player defined at the start of (3 4 13) at time 1
The pass defined at the start of (1 10 9) is blocked by the player defined at the start of (3 4 13) at time 2
We also mention the fact that passes can be intercepted at the beginning of the pass or at the end of the pass (imagine the blocker slides into the player that is to shoot/receive the ball)