408539: GYM103182 H Spies
Description
For his last mission in the espionage business, James Bond was tasked to determine how many spies he can send from the left side of the country to the right side, without raising any suspicions. The country has a total of N cities, where cities from $$$1$$$ to $$$\frac{N}{2}$$$ are placed on a line on the left side (ordered from $$$1$$$ to $$$\frac{N}{2}$$$), and cities from $$$\frac{N}{2} + 1$$$ to $$$N$$$ are on a line on the right side (ordered from $$$\frac{N}{2} + 1$$$ to $$$N$$$). There are no connections between cities on the same side of the country, but there are between cities on opposing sides, and between two cities, there can be at most one road that connects them.
Each road can only be travelled by one spy, and in order to not raise any suspicions, the roads of any two spies are not allowed to intersect, otherwise the enemy intelligence department would start thinking that the two are working together.
To clarify, James Bond is looking for a bipartite matching between the left side of the country and the right side, where no two roads intersect each other.
You are tasked to help James Bond find out the maximum number of spies he can send from the left side of the country to the right without raising suspicions, and in how many ways that can happen.
InputThe first line of the input contains two numbers, $$$2 \leq N \leq 2 \cdot 10^5$$$ and $$$1 \leq M \leq min(\frac{N^2}{4}, 10^6)$$$. $$$N$$$ is guaranteed to always be an even number.
The following $$$M$$$ lines each contain two numbers, $$$1 \leq A \leq \frac{N}{2}$$$ and $$$\frac{N}{2} + 1 \leq B \leq N$$$, meaning there is a road from city $$$A$$$ to city $$$B$$$.
OutputThe output files should contain two numbers, the maximum numbers of spies that can be sent without raising suspicions and the numbers of ways they can be sent. Because the ways they can be sent can become very large, you are asked to print it modulo $$$\mathbf{998244353}$$$.
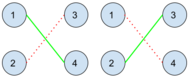
ExampleInput4 2 1 4 2 3Output
1 2Note
James Bond can only send at most $$$1$$$ spy, otherwise the roads they would intersect and would raise suspicions. There are $$$2$$$ ways in which James could send his spies.