408529: GYM103181 J Funny Tree

A funny tree is a perfect binary tree - that is, all of the internal vertices have two children and all of the leaves are situated at the same depth in the tree.

For a funny tree with $$$N$$$ levels, the root of the tree is labelled with $$$1$$$. For each node $$$x$$$ its children are labelled with $$$2 * x$$$ (left child) and $$$2 * x + 1$$$ (right child). See the diagram below for an example with $$$N = 3$$$.

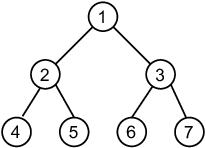
Moreover, a funny tree has friendships between some of its leaves. A friendship is defined as a pair $$$(x, y)$$$ where both $$$x$$$ and $$$y$$$ are leaves of the tree. We define the funness of a funny tree $$$T$$$ as:

• $$$F$$$ is the set of friendships of $$$T$$$
• $$$LCA(x, y)$$$ is the lowest common ancestor of nodes $$$x$$$ and $$$y$$$
• $$$SubtreeSize(z)$$$ is the number of nodes in the subtree of $$$T$$$ rooted at $$$z$$$

You are given a funny tree $$$T$$$ and its set of friendships $$$F$$$, as well as a number of operations. An operation can have one of the following types:

• type $$$0$$$: add new friendship $$$(x, y)$$$ to $$$F$$$
• type $$$1$$$: remove friendship $$$(x, y)$$$ from $$$F$$$
• type $$$2$$$: compute the funness of $$$T$$$ if leaves $$$x$$$ and $$$y$$$ are swapped (that is, if $$$x$$$ was placed where $$$y$$$ is in the original tree and the other way around)

The first line of the input contains an integer $$$N$$$ representing the height of the tree.

The second line of the input contains an integer $$$M$$$ representing the number of friendships.

The next $$$M$$$ lines contain the $$$M$$$ friendships $$$(x_i, y_i)$$$.

The following line contains an integer $$$Q$$$ representing the number of operations.

The last $$$Q$$$ lines of the input contain 3 integers $$$(t_i, x_i, y_i)$$$ representing the type of the operation and the two leaves for which the operation is intended.

$$$1 \leq N \leq 30$$$

$$$1 \leq M, Q \leq 10^5$$$

It is guaranteed that the initial $$$M$$$ friendships only contain leaves of the tree. Moreover, it is guaranteed that when the operation is to add a new friendship that friendship doesn't exist already in the set of friendships $$$F$$$. Likewise, when removing a friendship it is guaranteed that it exists in $$$F$$$. No friendship will be between a leaf $$$x$$$ and itself. Note that $$$(x, y)$$$ and $$$(y, x)$$$ represent the same friendship and it can appear in both forms in the input.

Note that operations of type $$$2$$$ leave the tree intact (no swap actually takes place).

The output should contain one integer per line representing the answers to the operations of type $$$2$$$ in the order they are received.

3
3
4 5
4 6
5 7
5
2 5 6
0 5 6
2 4 7
1 4 5
2 4 5

13
20
21